Il est clair que si les suites
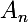
et
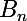
vérifient cette relation de récurrence, la suite
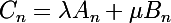
la vérifiera aussi. L'ensemble des suites vérifiant cette relation de récurrence est donc un espace vectoriel. On montre également que la dimension de cet espace est 3, et il est évident que les suites
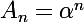
et
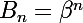
sont linéairement indépendantes dès l'instant que
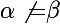
. Donc, si l'on trouve trois suites géométriques
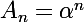
,
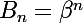
et
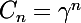
,
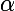
,
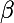
et
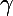
étant différents,
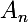
,
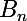
et
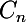
seront linéairement indépendantes et formeront donc une base de cet espace vectoriel. Par conséquent toute suite
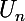
vérifiant cette relation de récurrence sera combinaison linéaire de ces trois suites. Les données de
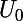
,
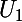
et
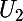
permettront alors de déterminer trois coefficients a, b et c tels que :
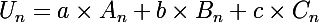
.
Tout cela est dans ton cours, je suppose.
Par conséquent la première chose à faire lorsque l'on est en présence d'une telle suite, est de chercher des suites géométriques vérifiant cette équation :
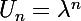
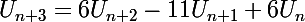
se traduit par :
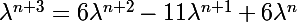
soit :
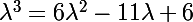
Il faut trouver des solutions de l'équation :
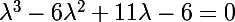
Comme 1 est racine évidente, on peut factoriser :
\times(\lambda^2-5\lambda+6)=0)
Et finalement, les racines du trinôme étant 2 et 3 :
\times(\lambda-2)\times(\lambda-3)=0)
On a donc trouvé trois valeurs de
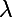
qui conviennent : 1, 2 et 3
Une base de l'espace vectoriel des suites vérifiant cette relation de récurrence est constituée par les trois suites :
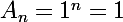
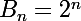
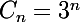
On peut donc exprimer
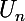
comme combinaison linéaire de ces trois suites :
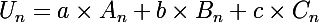
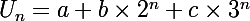
On sait que
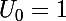
,
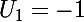
et
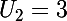
, par conséquent :
a+b+c=1
a+2b+3c=-1
a+4b+9c=3
ce qui fournit a=7, b=-10 et c=4.
Finalement :
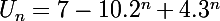
ce que l'on peut aisément vérifier.
Ce type de suite est directement issu de ton cours. Je t'engage à apprendre cette méthode une fois pour toutes de manière à ne plus être perdue la prochaine fois.
