Exo suite 1ere S

[girondin-62]

bonjour, suite a une petite absence de quelques jours en cours je comprend pas cet exercice sur les suites pourriez vous m'aider s'il vous plait, le voila:

v est la suite définie pour tout n par: Vn = (-2) à la puissance n
et w est la suite définie pour tout n par: Wn = 3n-5
Montrer que v est géométrique, puis que w est arithmétique
u est la suite définie pour tout n par : Un = (-2) puissance n + 3n-5
Calculer le réel S tel que: S= U2+U3+...+U10

voila j'espere que vous pourrez m'aider donc merci d'avance

[fatal_error]

Salut,

pour montrer qu'une suite est géométrique:
si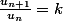 , k constant, est géométrique

pour montrer qu'une suite est arythmétique:
si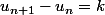 , k constant, est arythmétique.

Pour ce qui suit dans l'exo,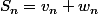
Or tu connais la formule de la somme des termes d'une suite géometrique, ainsi que celle pour les suites arythmétiques.

Bonne chance

[girondin-62]

ok, donc la je dois remplacer les Un par Vn et Wn selon ce que je dois démontrer?pour la quite aritjhmétique j'ai trouver par contre la suite géométrique je comprend toujours pas

[prof]

Pour la suite géométrique, tu calcules V(n+1)/V(n) et tu dois trouver une constante. Cela montre que la suite est géométrique