Pb integrale et suite

[seblemyxdu58]

bonjour j'ai un probleme pour deux question d'un dm

Pour tout entier naturel n, on pose In=intégrale(t^(n)*e^(t)dt) de 0 à 1

dans un premier temps on a démontrer que In=e-nI(n-1)
(I(n-1) veut dire I indice n-1)

qs : 1/ démontrer que la suite (In) est décroissante.
2/ Calculer integrale(t^(n)dt) de 0 à 1, puis démontrer que 0
pour integrale(t^(n)dt) de 0 à 1 j'ai trouvé (t²/2)-t
j'esper que vous pourrez m'aider
merci

[SimonB]

pour integrale(t^(n)dt) de 0 à 1 j'ai trouvé (t²/2)-t

Ca n'a pas de sens !!!

Le t est une variable muette (le "dt" signifie que t varie de 0 à 1), le résultat que tu dois trouver est un nombre (qui ne peut pas dépendre de t puisque t varie).

Prenons le problème dans l'autre sens : si g est une fonction définie par , peux-tu calculer la dérivée de g ? Peux-tu en déduire une primitive de la fonction f définie par ?

[seblemyxdu58]

une primitive de la fonction f(t)=t^n est la fonction F(t)=(t^n+1)/(n+1)

l'intégrale ca fait 1/(n+1) en fait nn?

[SimonB]

l'intégrale ca fait 1/(n+1) en fait nn?

Oui. Bien.

[seblemyxdu58]

pourriez vous m'indiquer comment commencer pour la question 1 pour prouver que (In) est décroissant parceque je bloque completement

[SimonB]

pourriez vous m'indiquer comment commencer pour la question 1 pour prouver que (In) est décroissant parceque je bloque completement

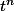
Si t est entre 0 et 1, peux-tu comparer les deux réels et ?

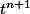
[seblemyxdu58]

entre 0 et 1 on a t^n+1donc t^n+1*e^t
donc In+1donc (In) est décroissante
est-ce juste?

[SimonB]

C'est juste.

[seblemyxdu58]

ok merci SimonB
pour la question deux je vois pas comment commencer, pouvez vouz m'aider?

[seblemyxdu58]

persone pour m'aider a la deuxieme question :cry:

[seblemyxdu58]

c bon g trouver merci pour tout merci SimonB