Problème 1ère S : sens de variation d'une suite

[Starwelle]

Bonjour !

Voila un exercice que j'ai à faire, mais où je butte sur la deuxième question :
1/ On note n! le produit des entiers de 1 jusqu'à n. Calculer 1!, 2!, 3!, 4!
2/ Etudier le sens de variation de la suite (Un) définie par Un = 2^n / n!

J'ai réussi la question 1 : 1! = 1 ; 2! = 2 ; 3! = 6 ; 4! = 24
Mais pour la 2ème question, je ne vois pas comment faire. Je pense qu'il faudrait étudier le signe de
Un+1 - Un, comme habituellement, mais je n'y arrive pas.

Merci d'avance de votre aide.

[vanouchka]

salut!
pr le sens de variation,je crois qu'il faut que tu trouves le signe de la raison.
peut etre que ta suite est géométrique,essaye (Un+1)/(Un).
essaye aussi de transformer l'écriture,des fois,on y voit plus clair pr la suite!bon courage!

[Sve@r]

Mais pour la 2ème question, je ne vois pas comment faire. Je pense qu'il faudrait étudier le signe de
Un+1 - Un, comme habituellement, mais je n'y arrive pas.

Merci d'avance de votre aide.

Tu ne peux pas le faire comme ça car l'opération "n!" n'est pas une opération instantanée (comme xy ou x^y). pour le trouver, il te faut énumérer et multiplier tous les naturels entre 1 et n. Les mathématiciens se sont d'ailleurs cassé la tête sur ce problème.

Et donc tu ne peux pas faire Un+1 - Un car tu pourras pas trouver un dénominateur commun entre n! et (n+1)! pour simplifier 2^n/n! - 2^(n + 1)/(n+1)!

Moi, je regarderais le taux de croissance entre 2^n et 2^(n+1) et entre n! et (n+1)! car ça c'est une opération possible. Si le taux est plus fort sur 2^n ça veut dire que le numérateur monte plus vite que le dénominateur donc le résultat de la division croit. Et sinon le résultat de la division décroit...

[SimonB]

C'est effectivement une démarche qui permet d'aboutir au résultat : . Réduis au même dénominateur (les deux dénominateurs sont très "proches") et factorise le numérateur. Le résultat vient en quelques lignes de calcul !

Cela dit, quand tu as des suites qui sont à termes positifs, il peut être bon d'essayer un critère par quotient : si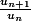 est plus grand que 1, la suite est croissante, si c'est plus petit que 1, elle est décroissante...

[SimonB]

Tu ne peux pas le faire comme ça car l'opération "n!" n'est pas une opération instantanée (comme xy ou x^y). pour le trouver, il te faut énumérer et multiplier tous les naturels entre 1 et n. Les mathématiciens se sont d'ailleurs cassé la tête sur ce problème.

J'avoue ne pas comprendre l'argument... De quoi parles-tu ? Cette méthode marche très bien (même si l'étude du quotient est bien plus simple).

[Sve@r]

C'est effectivement une démarche qui permet d'aboutir au résultat : . Réduis au même dénominateur (les deux dénominateurs sont très "proches")

Je suis très intéressé par l'opération "réduire deux divisions impliquant deux factorielles au même dénominateur (et surtout voir si ça se simplifie ensuite)...

[Starwelle]

Merci de vos réponses.

J'ai donc réessayer de travailler avec Un+1 - Un. Voila ce que j'obtiens avant d'être bloqué.

Un+1 - Un = (2^n x 2) / (n+1) ! - 2^n / n!
Je factorise donc :
2^n x ( 2/(n+1)! - 1/n!)

Comment puis-je continuer ?

[SimonB]

Un+1 - Un = (2^n x 2) / (n+1) ! - 2^n / n!
Je factorise donc :
2^n x ( 2/(n+1)! - 1/n!)

Comment puis-je continuer ?

Bien, si tu as commencé comme ça, continuons comme ça (ça marche effectivement).

Le facteur commun () est positif, il ne te reste plus qu'à étudier le signe de la parenthèse pour conclure.

Pour ce faire, remarque que et réduis au même dénominateur.

(D'autre part, je crois avoir vu passer, une fraction de seconde, un message de Sve@r qui s'interrogeait sur ma méthode. Où est-il passé ?)

[Sve@r]

J'avoue ne pas comprendre l'argument... De quoi parles-tu ? Cette méthode marche très bien (même si l'étude du quotient est bien plus simple).

Oui en y réfléchissant en fait les factorielles s'éliminent toutes seules. J'avais pas percuté et m'était focalisé sur la multiplication des dénominateurs...

Pour ce faire, remarque que (n+1)!=(n+1)* n! et réduis au même dénominateur.

(D'autre part, je crois avoir vu passer, une fraction de seconde, un message de Sve@r qui s'interrogeait sur ma méthode. Où est-il passé ?)

Ahah... les bienfaits de la suppression :zen:

[SimonB]

Oui en y réfléchissant en fait les factorielles s'éliminent toutes seules. J'avais pas percuté et m'était focalisé sur la multiplication des dénominateurs...

D'accord...

[Starwelle]

Ah! J'ai enfin réussi!
J'ai finalement fait avec le quotient. Tout se simplifiant beaucoup plus facilement !

Je vous remercie pour votre aide. Merci.