Bonjour,
Comment puis je montrer que (f1,f2,f3,f4) est une base de E?
Voici l'énoncé :
Soit F(R,R) le R-espace vectoriel des fonctions de R dans R. On considère les 4 éléments de F(R,R) suivants:
f1(x)=e^x
f2(x)=xe^x
f3(x)=e^(-x)
f4=(x)=xe^(-x)
Il faut montrer qu'ils sont linéairement dépendant c'est à dire qu'il existe une combinaison telle que af1+bf2+cf3+df4=0 avec a=b=c=d=0. Mais comment peut-on résoudre ce genre de système. Je pensais changer de variable, prendre X=e^x
C'est ça ?
Merci
Esapce vectoriel des fonctions
11 messages
- Page 1 sur 1
rougedemoiselle a écrit:Bonjour,
Comment puis je montrer que (f1,f2,f3,f4) est une base de E?
Voici l'énoncé :
Soit F(R,R) le R-espace vectoriel des fonctions de R dans R. On considère les 4 éléments de F(R,R) suivants:
f1(x)=e^x
f2(x)=xe^x
f3(x)=e^(-x)
f4=(x)=xe^(-x)
Il faut montrer qu'ils sont linéairement dépendant c'est à dire qu'il existe une combinaison telle que af1+bf2+cf3+df4=0 avec a=b=c=d=0. Mais comment peut-on résoudre ce genre de système. Je pensais changer de variable, prendre X=e^x
C'est ça ?
Merci
NON!
que la seule combinaison linéaire telle que af1+bf2+cf3+df4=0 est a=b=c=d=0.
Donc:
Tu ecris af1+bf2+cf3+df4=0 et tu montres que ça entraine: a=b=c=d=0.
bon travail
génération
Si tu montres que la famille est libre c'est insuffisant pour avoir une base car la famille doit etre génératrice.
Ou alors l'espace vectoriel étudié est de dimension 4 et ta famille libre est bien une base.
As tu plus de renseignements sur l'espace vectoriel E ?
Ou alors l'espace vectoriel étudié est de dimension 4 et ta famille libre est bien une base.
As tu plus de renseignements sur l'espace vectoriel E ?
harchymaide a écrit:Si tu montres que la famille est libre c'est insuffisant pour avoir une base car la famille doit etre génératrice.
Ou alors l'espace vectoriel étudié est de dimension 4 et ta famille libre est bien une base.
As tu plus de renseignements sur l'espace vectoriel E ?
Soit F(R,R) le R-espace vectoriel des fonctions de R dans R. On considère les 4 éléments de F(R,R) suivants:
f1(x)=e^x
f2(x)=xe^x
f3(x)=e^(-x)
f4=(x)=xe^(-x)
On pose E= Vect (f1,f2,f3,f4)
rougedemoiselle a écrit:Soit F(R,R) le R-espace vectoriel des fonctions de R dans R. On considère les 4 éléments de F(R,R) suivants:
f1(x)=e^x
f2(x)=xe^x
f3(x)=e^(-x)
f4=(x)=xe^(-x)
On pose E= Vect (f1,f2,f3,f4)
Par l'absurde, suppose qu il existe une combinason, t'as les possibilités suivantes : donne a x des valeurs particuliere, ou derive, ou fais tendre x vers + ou - infini c'est plus simple (apres q tu multiplie conveneblement par x et (ou exp(x) )
A-380 a écrit:Par l'absurde, suppose qu il existe une combinason, t'as les possibilités suivantes : donne a x des valeurs particuliere, ou derive, ou fais tendre x vers + ou - infini c'est plus simple (apres q tu multiplie conveneblement par x et (ou exp(x) )
Donc je pars par af1+bf2+cf3+df4 = 0 avec a=b=c=d=0.
Mais ensuite je ne vois pas du tout. Dsl
je ne sais pas faire une citation ...
tu dis
"Donc je pars par af1+bf2+cf3+df4 = 0 avec a=b=c=d=0.
Mais ensuite je ne vois pas du tout. Dsl"
pars seulement de
soit (a,b,c,d) de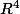 tels que af1+bf2+cf3+df4 = 0
tels que af1+bf2+cf3+df4 = 0
ceci est vrai pour tout x. a toi donc de choisir 4 valeurs de x pour trouver un système (si posssible simple) dont la résolution t'amèneras la nullité des coefficients.
tu dis
"Donc je pars par af1+bf2+cf3+df4 = 0 avec a=b=c=d=0.
Mais ensuite je ne vois pas du tout. Dsl"
pars seulement de
soit (a,b,c,d) de
ceci est vrai pour tout x. a toi donc de choisir 4 valeurs de x pour trouver un système (si posssible simple) dont la résolution t'amèneras la nullité des coefficients.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
