Domaine de validité fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 14 Avr 2008, 10:47
par Basse » 14 Avr 2008, 10:47
Quel serait le domaine de validité de la fonction :
(a-x)^(2/3) ?
Que peut on dire pour x>a ?
Merci de votre aide
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 14 Avr 2008, 10:48
par XENSECP » 14 Avr 2008, 10:48
passe à l'exponentielle (forme)
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 14 Avr 2008, 12:51
par Basse » 14 Avr 2008, 12:51
OK c'est vrai que c'est plus simple a manipuler mais quid du domaine de définition?
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 14 Avr 2008, 13:38
par nonam » 14 Avr 2008, 13:38
ben je vois pas où est le soucis.

est définie sur R. Donc elle est définie sur R.
A part ca, son graphe a une symétrie par rapport à l'axe "x=a". Donc l'étude peut se limiter à [a,

[
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 14 Avr 2008, 14:07
par Basse » 14 Avr 2008, 14:07
Ben j'ai l'impression que pour x>a ca pose probleme donc ca a pas la'ir defini sur R....
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 14 Avr 2008, 14:57
par nonam » 14 Avr 2008, 14:57
Pourrais-tu expliquer précisément le problème, car je ne vois pas...
exemples :
^{\frac{2}{3}})
= 1 , pour x>0 (ou pas),
^{\frac{2}{3}} = x^2)
etc...
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 14 Avr 2008, 15:26
par Basse » 14 Avr 2008, 15:26
Tout d'abord merci pour tes reponses
OK en fait tu veux dire que (-1)^(2/3) = ((-1)²)^(1/3). C'est ca?
Mais alors dans ce cas (-1)^(1/2)=((-1)²)^(1/4)=1 ce qui est faux.
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 14 Avr 2008, 16:32
par nonam » 14 Avr 2008, 16:32
De rien. Et en fait, la petite subtilité c'est que que pour un rationnel
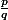
,
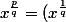^{p})
, et non :
^{\frac{1}{q})
. En tous cas, c'est comme ça qu'on l'a définit dans mon cours de sup. Du coup ,

est définit sur R+ si q est pair (non nul) , et sur R s'il est impair.
Et ton contre exemple n'est alors pas applicable...
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 14 Avr 2008, 16:48
par Basse » 14 Avr 2008, 16:48
En fait je suis d'accord avec tes explications mais quand je tape (-1)^(2/3) sur ma calculette j'ai un message d'erreur. Par contre (-1)^(1/3) pas de probleme.
et je viens de trouver (mais c'est peut etre pas vrai) que on a le droit de dire que a^(x . y) = (a^x )^y que si a est positif.
Qu'en penses tu?
Encore merci de ton aide
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 14 Avr 2008, 17:18
par nonam » 14 Avr 2008, 17:18
C'est vrai que a^(x . y) = (a^x )^y n'est vrai pour tout x et y, que si a>0.
Mais avec certains x et y , cette égalité est vrai pour tout a réel. Apparemment c'est vrai pour tout a, ssi

est bijective sur R.
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 15 Avr 2008, 09:21
par Basse » 15 Avr 2008, 09:21
Ainsi, cela veut dire que d'apres tes sources (cours de sup) x^(2/3) est defini sur R? J'insiste mais je trouve ca bizzare que la calculette donne un message d'erreur pour x<0 (mais pas pour x^(1/3))?
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 15 Avr 2008, 12:00
par nonam » 15 Avr 2008, 12:00
Oui, d'après mes sources, c'est bien ça. Mais bon, après je crois que ça dépend un peu des conventions. Y en a qui définissent les fonctions puissances seulement à partir des formes exponentielles, et donc ne les définissent que sur R+* (même les puissances entières).
Pour ce qui est des calculatrices, elles sont souvent peu fiables... Et j'ai essayé sur la mienne, elle trace bien

sur R entier. (TI 83+)
-
Basse
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Mai 2007, 16:24
-
 par Basse » 17 Avr 2008, 13:20
par Basse » 17 Avr 2008, 13:20
OK merci de ton aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
 sur R entier. (TI 83+)
sur R entier. (TI 83+)