Melange, barycentres, produits scalairs et limites

[youngforever]

Bonjour, voilà l'ennoncé du problème :

ABCD est un tétraède de l'espace. On note G son isobarycentre, I le milieu de [CD] et F le point de [AB] tel que F= 3/4AB( vecteur)
M est un point qui décrit un segment [AB] privé du point F. On se propose de déterminer l'ensemble E décrit pas le point d'intersection N de la droite (MG) et du plan (BCD)

( B, BA, BI) est un repère du plan ( ABG) M décrit le segment [ AB] privé de F. On note (x,o) les coordonnées de M et (o,y) les coordonnées de N.
a) à quel ensemble x appartient-il ?
b) Calculer les coordonnées de G, vecteurs MG et NG
c) en ecrivant que MG et NG sont colinéaires, exprimer y sous la forme y=f(x)
d) Etudier les variations de la fonction f, étudier sa limite en 1/4, dresser son tableau de variation
e) Conclure sur le lieu géometrique E décrit par N.

Je bloque complétement, est ce que quelqu'un pourrais m'aider s'il vous plait

[PONFIA]

Bonjour.

F le point de [AB] tel que F= 3/4AB( vecteur)

Commence par rectifier ton énoncé !!! Il manque une lettre !?

Je bloque complétement, est ce que quelqu'un pourrais m'aider s'il vous plait

Tu bloques où ? As-tu fais une figure ?

[youngforever]

Bonjour,

Il ne me semble pas qu'il manque une lettre !

Oui, j'ai fais une figure sur le logiciel geoplangeospace !

[youngforever]

En fait, j'ai calculé les coordonnées de G et trouve G (x,y) et ceux des vecteurs MG et NG tels que MG ( 0,y) et NG ( x, 0) mais je pense que je me suis trompée, car ensuite je n'arrive pas à prouver qu'ils sont colinéaires à l'aide de la formule x'y-xy'=0 , voilà..

[PONFIA]

Il ne me semble pas qu'il manque une lettre !

A mon avis, le point sur le segment est tel que et non tel que comme tu l'as marqué !


Sinon, qu'as tu trouvé pour la question a) ?

[youngforever]

J'avoue que je ne sais pas, je pensais que x appartenait à [AB] privé de F mais comme on me l'a fait remarqué, x est un nombre, il ne peut donc pas appartenir à un ensemble de point.

[PONFIA]

L'énoncé te dit que le point :
-- est sur le segment ;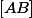
-- ses coordonnées dans le repère sont ;
-- est distinct du point .

Quelles sont les coordonnées (dans le repère ) des points 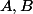et ?
Avec ça et compte-tenu de la relation tu devrais pouvoir trouver l'ensemble dans lequel le nombre appartient................

[youngforever]

A (1,0) B (0,0) F ( 0.25, 0) donc r appartient à [0, 1] privé de 0,25 ?

[PONFIA]

Ok ... on a donc .

Passes aux questions suivantes .....

[youngforever]

Pour la question suivante, comme on sait que G isobarycentre de A,B,C et D, il faut trouver les coordonnés des dits points afin de trouver ceux de G en utilisant la propriété des barycentres.

On a donc A ( 1,0) et B ( 0,0) mais je ne vois pas comment trouver C et D

[PONFIA]

Pour la question suivante, comme on sait que G isobarycentre de A,B,C et D, il faut trouver les coordonnés des dits points afin de trouver ceux de G en utilisant la propriété des barycentres.

Ok t'es sur la bonne voie,

[youngforever]

je crois que j'ai trouvé :

Soit G isobarycentre de A,B,C et D d'après la propriété d'associativité, G barycentre des points ( A,1) (B,1) ( I,2) avec A ( 1,0) B ( 0,0) et I(0,1)
on peut donc calculer : xg = 1/4 et yg= 2/4 donc les coordonnées de G sont G ( 1/4, 2/4 )

donc vecteurs MG ( 1/4 -x, 2/4 ) et NG ( 1/4, 2/4-y)

c'est juste ?

[youngforever]

mais après je ne trouve pas que les vecteurs sont colineaires à l'aide de la formule x'y- xy'= 0