Monte carlo

[mocine87]

salut si vous pouvez m'aider
*trouver un exemple d'un integrale calculer par la méthode Monte Carlo pour dimension 1 et 3 (Ret R3)
*Etudier convergence vers une valeur analytique en fonction de n

merci d'avance

[busard_des_roseaux]

euh, peut être simuler des tirages de trois v.a indépendantes x,y,z suivant la loi uniforme sur [0;1] et compter la fréquence de l'évènement:


ça devrait s'approcher de

[busard_des_roseaux]

re,
j'ai écrit une bêtise. Il faut qu'une fréquence ne dépasse pas 1.
Avec trois lois uniformes de v. a indépendantes X,Y,Z sur [0,1]
la fréquence de l'évènement



tend vers =volume sphère/volume cube

[BQss]

Salut, je me permets de poursuivre en donnant les deux exemples qui sont je crois les plus simples

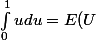avec U qui suit une loi uniforme sur [0,1]
l'estimateur MC est donc


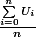
convergence de l'estimateur vers 1/2:
on utilise le théorème centrale limite et l'intervalle de confiance asymptotique:
l'IC asymptotique de probabilité alpha est de :



en prenant alpha =90% on a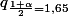
et donc:



donc convergence de l'ordre de

Ensuite

on fait exactement pareil pour la dimension 2 et 3, en prenant les lois uniformes produit respectives et leurs estimateurs respectifs(avec les variables uniformes indépendantes donc):

exemple pour la dimension 3

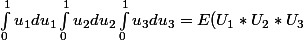, chaque 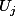suivant en fait une loi uniforme sur [0,1]
l'estimateur MC est donc


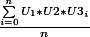
convergence de l'estimateur vers 1/8 (IC de 90%):



donc convergence de l'ordre de aussi.

Apres on peut inventer n'importe quoi, et pas qu'avec des lois uniformes!

a+ everybody