[Résolu] Calcul de 2 cos (2x - pi/4 ) = 0

[andy06]

Bonjour

J'ai un probleme pour resoudre cette équation.
Pouvez vous me dire ou est mon ereur
Car je ne trouve pas le bon resulta.

f(x)= 2 cos (2x - pi/4 )

Calcule de f(x)=0 sus ]0; pi/2[

2 cos (2x - pi/4 ) = 0

cos (2x - pi/4 ) = 0

2x - pi/4 = pi/2 [2pi] ou 2x - pi/4 = 3pi/2 [2pi]

2x = 3pi/4 [2pi] ou 2x = 7pi/4 [2pi]

x = 3pi/8 [2pi] ou 2x = 7pi/8 [2pi]

Merci d'avance

[saintlouis]

Bonsoir


C' est bon
Représente sur un cercle trigo..

[moutonjr]

[premier post effacé j'ai pas bien lu l'énoncé :triste: ]

Comme moi, n'oublie pas de voir le domaine de définition!
donc plus de 2k pi!
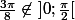
ensuite, euuh donc il n'y a plus qu'une solution? non?

[andy06]

Je comprend pas la.
3pi /8 appartient bien a l'intervalle, et 7pi/8 lui non.

Et je comprend pas car quand je remplace x dans le fonction ca me donne pas 0
Mais 2*10-14
Car je doit trouvé les cordonner de A

[fibonacci]

Bonjour;

en général pour des équations trigonométriques on trouve les résultats sous forme de radicaux, mais pas de valeur finie.
Coordonnée de A

Supprimé par la modération : dernier avertissement : on ne donne pas les solutions.

[andy06]

Ok merci beaucoup