salut, je propose quelque chose:
soit

comme f est continue sur

, elle l'est sur le compact [-T;2T].
La fonction f est donc uniformément continue sur [-T;2T]
Donc

tel que
 \in [-T;2T]^2, \|x-y\|\le \eta \Longrightarrow \|f(x)-f(y)\|\le \epsilon)
(*)
Soit
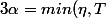)
(
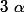
est strictement positif car

et T le sont)
Soit
\in \mathbb{R}^2)
tels que

Supposons que l'on ait
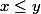
Il existe

tel que
T[)
Soit maintenant

et

On a:
1)

donc comme
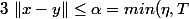)
, on a

et

2)

et comme

, on a

.
Finalement,
\in [-T,2T[)
Nous avons donc deux réels x' et y' tels que
\in [-T,2T[)
et

Donc en vertu de (*), on a
-f(y')\|\le \epsilon)
soit
-f(y-kT)\|\le \epsilon)
Par périodicité de f on arrive à
-f(y)\|\le \epsilon)
Finalement, on a montré que

,

, tel que
\in \mathbb{R}^2)
,
-f(y)\|\le \epsilon)
Donc f est uniformément continue sur
bye
:happy2:
