1ère S - Exercice suites et limites

[marineland]

Bonjour bonjour !
C'est encore moi ^^ et j'ai toujours un exercice pour mon DM de maths de jeudi que je n'arrive pas à résoudre

Voici l'énoncé:

La suite (Un) est définie pour tout n >= 1 (supérieur ou égal) par:
Un = [n/(n²+1)] + [n/(n²+2)] + ... + [n/(n²+n)]

1) Calculer U1,U2,U3 (sous formes de fractions irréductibles)
Mon résultat : U1 = 1/(1²+1) = 1/2
U2 = 2/(2²+2) = 2/6 = 1/3
U3 = 3/(3²+3) = 3/12 = 1/4

2)Un est la somme de n termes. Quel est le plus grand? le plus petit?
Mon résultat : plus grand terme => Un = n/(n²+1)
plus petit terme => Un = n/(n²+n)

3) En déduire que pour tout n>= 1 (supérieur ou égal), n²/(n²+n) < Un < n²/(n²+1)
Mon résultat : c'est la que je bloque car il est facil de dire que Un est compris entre n/(n²+n) et n/(n²+1) mais comment faire pour prouver avec le n² en haut ???

4)Quelle est alors la limite de la suite (Un) ? Justifier.
Mon résultat : il faut utiliser le théorème des gendarmes (ou théroème d'encadrement) ... mais je planche un peu sur la limite de nos deux termes ...


Voilà merci d'avance pour votre aide !

[SimonB]

Bonjour,

Bonjour bonjour !
C'est encore moi ^^ et j'ai toujours un exercice pour mon DM de maths de jeudi que je n'arrive pas à résoudre

Voici l'énoncé:

La suite (Un) est définie pour tout n >= 1 (supérieur ou égal) par:
Un = [n/(n²+1)] + [n/(n²+2)] + ... + [n/(n²+n)]

1) Calculer U1,U2,U3 (sous formes de fractions irréductibles)
Mon résultat : U1 = 1/(1²+1) = 1/2
U2 = 2/(2²+2) = 2/6 = 1/3
U3 = 3/(3²+3) = 3/12 = 1/4

Euh, non ! Pour U1, c'est juste, mais ...

2)Un est la somme de n termes. Quel est le plus grand? le plus petit?
Mon résultat : plus grand terme => Un = n/(n²+1)
plus petit terme => Un = n/(n²+n)

C'est juste.

3) En déduire que pour tout n>= 1 (supérieur ou égal), n²/(n²+n) < Un < n²/(n²+1)
Mon résultat : c'est la que je bloque car il est facil de dire que Un est compris entre n/(n²+n) et n/(n²+1) mais comment faire pour prouver avec le n² en haut ???

Tu sommes n termes. Le résultat de la somme est plus petit que n*(le plus grand terme dans ta somme), et plus grand que n*(le plus petit terme de ta somme) !

4)Quelle est alors la limite de la suite (Un) ? Justifier.
Mon résultat : il faut utiliser le théorème des gendarmes (ou théroème d'encadrement) ... mais je planche un peu sur la limite de nos deux termes ...

Tu dois avoir dans ton cours quelque chose qui te dit que quand tu as un polynôme sur un autre polynôme, la limite est déterminée par le terme de plus haut degré du numérateur et du dénominateur (écrit précisément : si , alors la limite de la suite est la même que la limite de .

[marineland]

ok pour la question 1, je me suis pas rendue compte de l'erreru quej 'avais fais ...
par contre ya rien dans mon cours qui parle de polynome bizarre pour la question 4 ...

[marineland]

Après reflexion je me rends compte que je ne comprends pas non plus ta réponse à la question 3 ... :S

[SimonB]

Bien : je réexplique :happy2:

Pour la question 3 :
est définie comme la somme de n termes positifs : .

On va les appeler autrement : tu appelles le premier terme , le deuxième terme 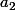, ..., le n-ième terme .

Tu as donc .

Ce que tu as montré, c'est que était le plus grand des termes .

Il suffit alors de prouver que est inférieur à . Vois-tu pourquoi c'est vrai ? (Si non, commence par des cas particuliers : n=2, 3...)

Tu fais la même chose pour l'autre inégalité avec le plus petit.


Pour la question 4, bon, c'est ennuyeux si tu ne connais pas ces résultats-là...

Enfin, bon, on va le faire "avec les mains" : les trucs qui encadrent ta suite, c'est et .
Est-ce que tu n'as pas une petite idée de la limite vers laquelle ces machins-là peuvent tendre ?

Le plus grand par exemple, . Quand n est très grand (tend vers l'infini), est-ce que est "proche" ou "loin" de 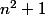? Aurais-tu une idée de ce que vaut (ou est proche de valoir) le quotient des deux ? On regardera plus tard pour le premier terme...

(Attention, tout ce que je raconte, c'est de la bidouille et pas des preuves sérieuses. C'est juste pour te faire sentir ce qui se passe dans ces quotients. C'est l'important à comprendre, après on s'attelle à des preuves, mais si tu vois pas comment l'affaire marche, tu n'auras rien retiré de l'exercice...)

[marineland]

Non je comprends toujours aucune des deux réponses ...
Est-ce que tu peux me donner ce qu'il faut que je mette sur ma copie et j'essayerais de comprendre plsu tard stp ?
Parce que là ça devient très urgent :s

Merci

[Dominique Lefebvre]

Non je comprends toujours aucune des deux réponses ...
Est-ce que tu peux me donner ce qu'il faut que je mette sur ma copie et j'essayerais de comprendre plsu tard stp ?
Parce que là ça devient très urgent :s

Merci

Bonsoir,
Je crains fort que tu ne sortes des règles et surtout de l'esprit du forum! Comme te l'a écrit très justement SimonB, le but est que tu comprennes, pas que tu recopies bêtement un truc trouvé sur le forum.
Il va donc falloir que tu fasses un effort pour finir ton devoir avec les explications qu'on te donne....

Pour la modération.

[marineland]

Désolée ...
J'essaie deocmprendre c'est pour ça que je viens ici parce qu'il faut que je rattrape une mauvaise que j'ai eu au dernier dm ...
Bon je faire avec ce qu'il me donne ...

En tout cas MERCI !

[marineland]

Aprés reflexion j'ai compris :D
Et désolée pour ce petit coup de "feignantise" en fait j'ai réussi à me débrouiller avec les pistes de Simon B alors MERCI beaucou p !!!!! :we:

[Dominique Lefebvre]

Aprés reflexion j'ai compris
Et désolée pour ce petit coup de "feignantise" en fait j'ai réussi à me débrouiller avec les pistes de Simon B alors MERCI beaucou p !!!!! :we:

Bravo! Compte sur moi pour te faire regretter tes coups de fainéantise... Ce qui est bien en math, c'est que le travail rapporte toujours )

[SimonB]

Je t'en prie. C'est toujours un plaisir quand on réussit à faire comprendre quelque chose :)