bonjour
je cherche a calculer la somme des séries suivantes :
1) n.a^n-1
2) n².a^n-1
pour la premiere, j'aurais tendance à dire que c'est la série entière dérivée de la série x^n, série dont la somme infinie est 1/1-x
donc je dirais que la somme de la série n.a^n-1 est la dérivée de (1/1-a), mais je ne suis pas sur.
par contre, pour la 2), je ne vois pas du tout :(
merci beaucoup
Somme de séries
3 messages
- Page 1 sur 1
max a écrit:bonjour
je cherche a calculer la somme des séries suivantes :
1) n.a^n-1
2) n².a^n-1
pour la premiere, j'aurais tendance à dire que c'est la série entière dérivée de la série x^n, série dont la somme infinie est 1/1-x
donc je dirais que la somme de la série n.a^n-1 est la dérivée de (1/1-a), mais je ne suis pas sur.
par contre, pour la 2), je ne vois pas du tout
merci beaucoup
n² = n(n-1) + n
bonjour,
c'est bien ce que tu as pensé.
Serie entieree (a_n=1) donc tu peux y aller a la derivation terme a terme.
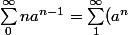'=(\sum_1^{\infty} a^n)'=(\frac{a}{1-a})')
Pour la seconde, c'est un peu crapuleux.
Faudrait que tu partes dun a^{n+1} quand tu dérives double, tu as dua^{n-1}) en developpant tas
en developpant tas  que tu connais. Apres te reste a faire la différence.
que tu connais. Apres te reste a faire la différence.
c'est bien ce que tu as pensé.
Serie entieree (a_n=1) donc tu peux y aller a la derivation terme a terme.
Pour la seconde, c'est un peu crapuleux.
Faudrait que tu partes dun a^{n+1} quand tu dérives double, tu as du
la vie est une fête 
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
