Resultat evidente mais demonstration difficile pour moi : se
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
badola
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Fév 2008, 05:11
-
 par badola » 23 Mar 2008, 22:35
par badola » 23 Mar 2008, 22:35
Bonsoir a tous:
Voici une question evidente que j'ai de difficulte a montrer proprement:
Soit une serie entiere
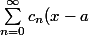^n)
de rayon de convergence
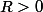
tel que au moins

est
non nul. .
Montrer qu'il existe un nombre reel

,

tel que la somme de la serie entiere est non nulle pour tout reel

tel que

.
J'ai essayer de faire une demonstration par l'absurde mais ca ne marchait pas.
Besoin d'indications.
MERCI beaucoup
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 23 Mar 2008, 22:39
par Joker62 » 23 Mar 2008, 22:39
Une somme de série entière est identiquement nulle si et seulement si tous ses coefficients sont nuls !
Il faut donc montrer que si f est une somme de série entière non identiquement nulle, alors il existe un voisinage de a dans lequel f ne s'annule pas du tout !
Et là, on parle de zéros isolés.
Tu peux compléter tes recherches maintenant.
 par alavacommejetepousse » 23 Mar 2008, 23:32
par alavacommejetepousse » 23 Mar 2008, 23:32
bonsoir
sans parler de zéros isolés j'aurais dit:
quitte à simplifier par un (x-a)^n on peut supposer c0 non nul et alors la somme étant une fonction CONTINUE ne s'annulant pas en a ne s 'annule pas sur toute une boule de centre a.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Mar 2008, 09:35
par ThSQ » 24 Mar 2008, 09:35
alavacommejetepousse a écrit:ne s 'annule pas sur toute une boule de centre a.
Certes mais le résultat demandé est plus fort il me semble ...
 par alavacommejetepousse » 24 Mar 2008, 09:46
par alavacommejetepousse » 24 Mar 2008, 09:46
ThSQ a écrit:Certes mais le résultat demandé est plus fort il me semble ...
Ben non c'est exactement le résultat demandé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités