Cône

[legeniedesalpages]

Bonjour,

j'ai un souci avec cet exo:

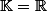
Soient un -espace vectoriel ( ou ).

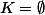
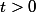
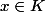
On dit qu'un sous-ensemble de est un cône quand ou quand pour tout réel et tout point , on a .

1) La réunion d'une famille de cônes fermés de est-elle un cône fermé de ?

2) La réunion d'une suite croissante de cônes fermés de est-elle un cône fermé de ?

Merci pour votre aide.

[alavacommejetepousse]

bonjour

la stabilité est claire

r n la suite des rationnels
dans le plan Dn la demi droite d'origine O d'angle r n la réunion des Dn n'est pas fermée.

[E#Mc²]

Bonjour,

j'ai un souci avec cet exo:

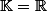
Soient un -espace vectoriel ( ou ).

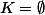
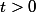
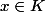
On dit qu'un sous-ensemble de est un cône quand ou quand pour tout réel et tout point , on a .

1) La réunion d'une famille de cônes fermés de est-elle un cône fermé de ?



2) La réunion d'une suite croissante de cônes fermés de est-elle un cône fermé de ?

Merci pour votre aide.

Pour 2) consider IR, puis les demi intervalles fermés [1/n , +infini [ , le reunion est ]0, + infini [

[ThSQ]

Non pour le 1) : prendre les 1/2-droites réelles a*x avec a >= 0 et x >= 0, on obtient un 1/4 plan non fermé.

J'ai envie de dire non pour le 2) mais je vois pas de contrex pour le moment

[ThSQ]

A oui E#Mc² a donné un contrex d'une remarquable simplicité ! :++:

[legeniedesalpages]

Pour 2) consider IR, puis les demi intervalles fermés [1/n , +infini [ , le reunion est ]0, + infini [

[1/n , +infini [ est un cône?

[ThSQ]

[1/n , +infini [ est un cône?

lol, trop simple pour être vrai !

[legeniedesalpages]

bon merci, pour les contrex de la 1) j'ai compris :)

Après, reste à voir pour la 2)

[legeniedesalpages]

Non pour le 1) : prendre les 1/2-droites réelles a*x avec a >= 0 et x >= 0, on obtient un 1/4 plan non fermé.

J'ai envie de dire non pour le 2) mais je vois pas de contrex pour le moment

Si on reprend cet exemple:


on prend l'union des 1/2-droites réelles a*x telles que , x >= 0, on le note .

est fermé, l'union des est croissante, et égale au même quart de plan non fermé, non?

[alavacommejetepousse]

mon contre exemple ne vous allait pas ...

[legeniedesalpages]

mon contre exemple ne vous allait pas ...

pour la 1) si, il me va très bien.

[ThSQ]

mon contre exemple ne vous allait pas ...

Perso, j'avais pas vu ton post quand j'ai posté et j'ose imaginer qu'on est autorisé à poster même après que Tu As Parlé ! :ptdr:

Pour le deux, on peut prendre les parties du plan entre la 1/2 droite {y=0,x>=0} et la 1/2 droite { y = n*x, x >= 0 }. Pareil leur union donne 1/4 plan non fermé.

[alavacommejetepousse]

Perso, j'avais pas vu ton post quand j'ai posté et j'ose imaginer qu'on est autorisé à poster même après que Tu As Parlé ! :ptdr:

.

mais certainement ; si ce n'est que tu as bien vu un contre exemple d'une remarquable simplicité;