Exposants de (-1)

[Memento]

Bonjour à tous !

Pourriez-vous m'aider à simplifier cette formule:



puis-je écrire



=



=

-


Je suis bien conscient qu'il vaudrait mieux utiliser la notation d'Euler pour ce genre de calculs ( )

Merci beaucoup

@+

[alavacommejetepousse]

bonsoir

(-2)^(0,25) n'est pas défini.

[Memento]

J'en suis bien conscient

Je souhaite simplement ramener cette expression à un nombre "complexe"...

genre:


)

[busard_des_roseaux]

Bonjour à tous !

Pourriez-vous m'aider à simplifier cette formule:



[/TEX] )

Bjr,

examinons ce qu'est une détermination du log complexe:
si z et u sont deux nombres complexes, calculer log(z)
c'est résoudre l'équation d'inconnue u=x+iy
.

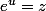
Il vient:



On montre que l'on a une détermination continue de l'argument de z,
quand z appartient à un ouvert simplement connexe de , ce qui veut dire que est alors une mesure d'angle qui est univoque et qui varie continuement en fonction de z.

on considère l'ouvert de :

privé de la demi-droite

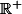
l'argument de z varie alors de quand z appartient à cet ensemble ouvert.

Dans ce genre de considération, on ne raisonne pas du tout "modulo 2 pi"
comme d'habitude, mais au contraire, on suit continuement l'argument
de z quand il se déplace dans l'ouvert (ou sur la surface de Riemann).

Sans utiliser les log, on a

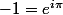
d'où on trouve comme résultat:




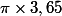
Comme l'argument est sorti
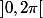
du domaine de définition , on est bien ennuyés. :hum:

Le problème, c'est qu'à cet argument
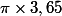
on pourrait rajouter:

avec pour obtenir d'autres résultats.

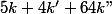
Les entiers forment le sous-groupe tout entier.

Le produit est donc une famille de complexes de module

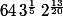
et d'arguments:

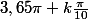
Sur la surface de Riemann du log, ils sont situés sur une hélice à intervalles réguliers. Il faudrait voir comment ils se situent sur les différents feuillets.

[Memento]

Merci beaucoup pour votre exposé !

Je me permet de vous envoyer un message privé ou je vous précise mon problème.

Merci encore.