Espaves vectoriels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cece71
- Membre Naturel
- Messages: 36
- Enregistré le: 03 Jan 2007, 18:09
-
 par cece71 » 11 Mar 2008, 16:12
par cece71 » 11 Mar 2008, 16:12
Soit A={f continue sur [0,1] tq intégrale (0 à 1/2) f(t)dt - intégrale(1/2 à 1) f(t) dt =1}
Il faut monter que A est une partie fermée et convexe qui ne contient aucun élément de norme minimal.
La norme infinie est elle une norme associée à un produit scalaire??
J'ai réussi à montrer que A est un fermé et convexe, mais je n'arrive pas la suite.
Un petit coup de main serait utile, merci.
 par Francisfrancis » 11 Mar 2008, 16:28
par Francisfrancis » 11 Mar 2008, 16:28
c'est trivial, cherchez un peu vous allez trouvé. :marteau:
-
cece71
- Membre Naturel
- Messages: 36
- Enregistré le: 03 Jan 2007, 18:09
-
 par cece71 » 11 Mar 2008, 16:29
par cece71 » 11 Mar 2008, 16:29
???????????
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Mar 2008, 18:01
par yos » 11 Mar 2008, 18:01
Bonsoir.
fermée : image réciproque d'un fermé par une application C°.
Convexe : preuve directe avec tf+(1-t)g.
A est stable par ajout de constante donc on peut descendre autant qu'on veut en norme.
La norme infinie vérifie-t-elle l'identité du parallélogramme?
-
cece71
- Membre Naturel
- Messages: 36
- Enregistré le: 03 Jan 2007, 18:09
-
 par cece71 » 11 Mar 2008, 18:41
par cece71 » 11 Mar 2008, 18:41
euh,jcompren pa tro kan tu di : A est stable par ajout de constante??Quel rapport avec les normes et le fait que A ne contient aucun élément minimal??
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Mar 2008, 19:35
par yos » 11 Mar 2008, 19:35
Je suis pas sûr du rapport immédiat. D'abord quelle est la norme sur C°?
Sinon je dis que si
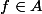
, alors f-5, f+7, f-35 ... sont aussi dans A.
 par Francisfrancis » 12 Mar 2008, 16:06
par Francisfrancis » 12 Mar 2008, 16:06
Vive la gym d'entretien... :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
