:briques: voila je suis en premiere S et je bloque completement sur les polynomes. j'ai essayer en vin de faire cet exercice alors si quelqu'un pouvais m'aider car a chaque fois la solution que je trouve n'est pas corecte. Merci d'avance
Déterminer a,b et c de sorte que pour tout réel x :
(2x^3+4x^2-4x-2) = (x-1) * ( ax^2+bx+c)
( les ^ annonce la puissance ex : 2^2 c'est 2 au carrée )
Polynomes (petit soucis)
9 messages
- Page 1 sur 1
Ce genre d'exos est très courant. La question est qu'esce que je veux chercher exactement?
=> Les valeurs de a , b et c
En général, on utilise le fait que deux polynomes sont egaux si et seulement si leurs coefficients des termes de meme degrés sont égaux. Tu dois donc trouver des égalités du type a= ?? , b= ?? etc
Comment faire? Il faut revenir a une égalité ou tu auras de chaque coté des , des
, des  des x et des nombres reels.
des x et des nombres reels.
Pour cela, tu peux appliquer cette méthode:
tu développes le membre de droite:
\times (ax^2+bx+c)= ax^3+bx^2+cx-ax^2-bx-c.)
Tu factorise par x ce que tu peux pour des coeeficients de meme degré:
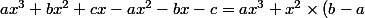+x \times (c-b)-c)
Tu sais que cette derniere expression est égale a 2x^3+4x^2-4x-2
tu peux donc ecrire:

+x \times (c-b)-c)
Par identification des termes de meme degrés on a :
a=2 a=2 a=2
b-a=4 b=a+4 b=6
c-b=-4 -b=-4-c c=2
-c=-2 c=2
Donc =
= (2x^2+6x+2))
Tu peux toujours verifier en redeveloppant. Essaye de bien comprendre ce genre d'exos ca revient très souvent et particulierement pour trouver les racines d'un polynome de degrés 3
@+ :happy2:
=> Les valeurs de a , b et c
En général, on utilise le fait que deux polynomes sont egaux si et seulement si leurs coefficients des termes de meme degrés sont égaux. Tu dois donc trouver des égalités du type a= ?? , b= ?? etc
Comment faire? Il faut revenir a une égalité ou tu auras de chaque coté des
Pour cela, tu peux appliquer cette méthode:
tu développes le membre de droite:
Tu factorise par x ce que tu peux pour des coeeficients de meme degré:
Tu sais que cette derniere expression est égale a 2x^3+4x^2-4x-2
tu peux donc ecrire:
Par identification des termes de meme degrés on a :
a=2 a=2 a=2
b-a=4 b=a+4 b=6
c-b=-4 -b=-4-c c=2
-c=-2 c=2
Donc
Tu peux toujours verifier en redeveloppant. Essaye de bien comprendre ce genre d'exos ca revient très souvent et particulierement pour trouver les racines d'un polynome de degrés 3
@+ :happy2:
(2x^3+4x^2-4x-2) = (x-1)*(ax^2+bx+c)
Tu développes d'abord cette partie (x-1)*(ax^2+bx+c)
Ce qui te donne normalement ax^3+(b-a)x^2+(c-b)x-c
Pour tout réel x,
ax^3+(b-a)x^2+(c-b)x-c = (2x^3+4x^2-4x-2)
si et seulement si, a= 2 a=2
b-a= 4 b=6
c-b= -4 c=2
Je crois que c'est ça mais je ne suis pas sûr, d'autres personnes ont sans doute une meilleure solution :happy2:
Tu développes d'abord cette partie (x-1)*(ax^2+bx+c)
Ce qui te donne normalement ax^3+(b-a)x^2+(c-b)x-c
Pour tout réel x,
ax^3+(b-a)x^2+(c-b)x-c = (2x^3+4x^2-4x-2)
si et seulement si, a= 2 a=2
b-a= 4 b=6
c-b= -4 c=2
Je crois que c'est ça mais je ne suis pas sûr, d'autres personnes ont sans doute une meilleure solution :happy2:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
