Polynome de degré 3

[lerital]

[FONT=Comic Sans MS]Je suis bloqué sur un exercice de maths, voici le polynome:
E) x^4- 4x^3 +2x²-4x+1 =0
Apres avoir vérifier que 0 n'étais pas solution de ce polynome, on me demande de démontrer que si u est solution de E alors (1/u) est aussi solution de E.
Je suis bloqué, pouvez vous me donner des conseils pour que je puisse continuer l'exercice sur de bonnes bases??
Merci d'avance !! :id: [/FONT]

[Alpha]

Ton polynôme est un polynôme symétrique, ce qui veut dire que ses coefficients sont symétriques. Ici, tes coefficients sont : , , , , .

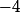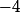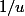Dans ce cas, quand est solution, est toujours solution (on te demande de vérifier que si est solution, est non nul, pour pouvoir poser 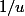. Mais dans le cas d'un polynôme symétrique non nul, comme le terme constant est égal au coefficient du terme de plus haut degré qui est par définition non nul, ce terme constant est non nul, donc 0 n'est pas solution).

Ici, c'est bien simple :tu supposes solution, et tu remplaces par 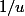dans l'expression . Il suffit alors de tout multiplier par pour se rendre compte que le tout est égal à , donc que 1/u est bien solution de E.

Alpha +