Bonjour je narrive pas a montrer par récurrence sur n la formule suivante
Supposons que S = Somme sigma
Pour tout n appartien a N
n
S k/2^k=4-(2-n+2/2^(n-1))
k=0
Merci de m'aider
Par ou commencer?
Suites récurrentes
8 messages
- Page 1 sur 1
ah oui je me suis trompé voici la formule exacte
Pour tout n appartient a N
n
S k/2^k= 4 -(n+2/ 2^(n-1))
k=0
Si vous faites attention a toutes les parenthèses normalement c'est bon
je précise que le n-1 est en indice
ainsi que le k dans 2^k
Et que (n+2/ 2^(n-1)) est une fraction donc 4 moins tout le tralala
S représente Somme, sigma
Pour tout n appartient a N
n
S k/2^k= 4 -(n+2/ 2^(n-1))
k=0
Si vous faites attention a toutes les parenthèses normalement c'est bon
je précise que le n-1 est en indice
ainsi que le k dans 2^k
Et que (n+2/ 2^(n-1)) est une fraction donc 4 moins tout le tralala
S représente Somme, sigma
Salut, je m'exprime sans doute mal. Pour trouver la formule j'ai calculé 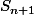 en fonction de
en fonction de 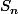 de deux manières. Et j'ai utilisé un changement de variable type K=k+1.
de deux manières. Et j'ai utilisé un changement de variable type K=k+1.

Mais on a aussi
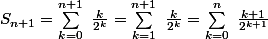 ("décalcage d'indice" si ça se dit)
("décalcage d'indice" si ça se dit)
D'où
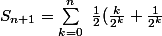= \frac{1}{2} S_{n}\ + \ 1 - \frac{1}{2^{n+1}})
Et le résultat suit. Tu peux par exemple calculer la somme des n premières puissance de 2, de 3 etc... avec cette methode (en anglais ils disent methode des perturbations)
Mais on a aussi
D'où
Et le résultat suit. Tu peux par exemple calculer la somme des n premières puissance de 2, de 3 etc... avec cette methode (en anglais ils disent methode des perturbations)
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
