Dm de maths..fonction ln

par **vévé** » 29 Oct 2005, 17:20

voila juste une question:
comment faire pour dériver cette fonction de la forme u/v?
f(x)= 1+2lnx / x^2n
merci beaucoup

par **Galt** » 29 Oct 2005, 17:25

Bonjour
Ca manque de parenthèses, mais j'aurais tendance à exploiter les formules suivantes :
Dérivée de

:

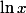
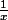
Dérivée de

:

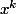
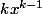
(prends

)
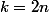
Dérivée de

:

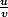
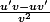
Voila

par **vévé** » 29 Oct 2005, 17:37

ben dsl pour les parenthèses..sinon c'est ce que j'ai fais pour dériver..mais j'aimerais comparer votre ultime calcul...je trouve:

2[1-nx^n-1(1+lnx)]/x^3n

mer6.........:)

par **Galt** » 29 Oct 2005, 17:55

Tout dépend de l'expression de f : Si

Alors c'est parti :

sauf erreur

par **Galt** » 29 Oct 2005, 18:10

Mais on peut aussi avoir

et là ce n'est plus pareil

par **vévé** » 29 Oct 2005, 18:24

Galt a écrit:Mais on peut aussi avoir et là ce n'est plus pareil

ben cest celui ci de calcul..cest de ma faute j'ai oublié les parenthèses

par **Galt** » 29 Oct 2005, 18:41

Alors allons y

par **vévé** » 29 Oct 2005, 19:33

Galt a écrit:Alors allons y

ca serait possible que tu me detailles les calculs??
merci beaucoup

par **Galt** » 29 Oct 2005, 19:51

Galt a écrit:Alors allons y

Je mets

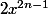
en facteur au numérateur :

, puis ensuite je simplifie

par **vévé** » 29 Oct 2005, 20:02

merci beaucoup!!
bonne soiré et a bientot.. ;)

Dm de maths..fonction ln

Dm de maths..fonction ln

Qui est en ligne