Base et espace vectoriel

[math*]

Bonjour je suis en mpsi et jai besoin de votre aide pour un exo dont voici l'énoncé.
Donner une condition nécessaire et suffisante sur pour que admette une base formée de polynomes sans racines réelles.

Je ne vois vraiment pas quoi faire. Merci de votre aide.
Cordialement.

[busard_des_roseaux]

Bonjour,

Un polynôme de degré impair a une racine réelle à cause du TVI.

je subodore que n doit être pair.

Ce que je commencerai à faire:

construire une famille libre de polynomes de degrés pairs
sans racines réelles de degrés dans

essayer de bidouiller pour obtenir les monômes de degrésimpairs

[math*]

Certes c'est nécessaire mais tu crois que c'est suffisant ?
Si oui une petite idée de démo ? Parce que moi à première vue je ne vois vraiment pas. :briques:

[busard_des_roseaux]

la famille est libre car tous les degrés sont distincts.

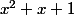
le trinome est tjrs strictement positif.
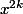
On le multiplie par . Il reste positif.
on ajoute 1.

ne s'annule pas,
pour tout .

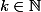
je me demande si ainsi on "récupère" les monomes de degré impairs.
La réunion des deux familles répondrait à la question.

[math*]

Je suis d'accord avec ce que tu as dit mais je ne comprends pas en quoi ça répond à la question. On veux que la famille soit une base et je ne vois pas du tout comment montrer que la réunion de tes 2 familles est une base de Rn[X].. Merci de m'éclairer :id: :we:

[busard_des_roseaux]

je ne vois pas du tout comment montrer que la réunion de tes 2 familles est une base de Rn[X]..

elle est clairement génératrice.

[math*]

Oui oui bien sur autant pour moi j'avais pas bien regardé. :dodo:

Par contre en effet il faut voir si on peut avoir du degré impair. ça paraît bien en soustrayant le polynome de degré le plus haut de la première famille avec le polynome de degré le plus haut de la seconde. On fait ainsi "partir" le terme de plus haut degré qui se trouve être pair et il reste le terme impair qui provient du polynome de la seconde famille...
On a ainsi des polynomes de degré impair.
Alors la par contre si j'écris ça mon prof va être content ( :ptdr: ).
Mais l'idée est là n'est-ce pas ? :hum:

[busard_des_roseaux]

Par contre en effet il faut voir si on peut avoir du degré impair. ça paraît bien en soustrayant le polynome de degré le plus haut de la première famille avec le polynome de degré le plus haut de la seconde. On fait ainsi "partir" le terme de plus haut degré qui se trouve être pair et il reste le terme impair qui provient du polynome de la seconde famille...
On a ainsi des polynomes de degré impair.
Alors la par contre si j'écris ça mon prof va être content ( :ptdr: ).

je ne crois pas :hum:

Il suffit de montrer que tout monôme de la forme
est combinaison linéaire de vecteurs de la réunion des deux familles.

Si on regarde les polynomes de la seconde famille, à part le terme
tous lesd autres monomes sont de degré pair.

[math*]

Oui oui c'est un peu ce que j'avais dit mais c'est vrai que c'était incompréhensible. :hum: