Besoin d'aide pour un problème d'optimisation =D [ résolu !!

[Sowsow]

Bonjour tout le monde,

Etant en 1ere S, je sollicite votre aide pour une question d'un exercice de mon DM à rendre pour la rentrée et sur laquelle je bloque énormément :mad2:

Voici l'énoncé :

( V= racine carrée )

Dans un triangle ABC rectangle en A tel que AB=3V3 et l'angle ABC = PI / 6 , on place un point P sur l'hypoténuse de ce triangle. On appelle I et J les projetés orthogonaux respectifs de P sur [AB] et [AC].

Problème :

Où faudrait-il placer le point P pour que le segment IJ soit le plus court possible ?

_______________________________________________

J'ai modélisé l'énoncé grâce à Géogébra etc ...
Mais je n'arrive pas à trouver le lien entre x et y. ( soit x = [BP] et y = [IJ] ) ...

Je ne sais vraiment pas quelle formule utilisée :S et je m'arrache littéralement les cheveux ...
Et sans une écriture du type y= ....x.... , je ne peux étudier la fonction et trouver le minimum ( et donc répondre au problème ).

Voilà je vous demande juste de m'éclairer sur la formule à utiliser .. ( Al Kashi ?? )
Merci d'avance ...

[emdro]

Bonjour,

dans le rectangle AIPJ, les diagonales sont de même longueur, non?

[Sowsow]

Merci de répondre aussi vite =)
Oui c'est exact. On a bien JI = AP.

Mais quel est le lien entre AP et PB alors ?

Je pensais utiliser une formule que me permettrait d'avoir IJ en fonction de PB puis d'étudier la fonction ... ( trouver son minimum et donc la réponse à la question posée ).

Merci beaucoup.

[emdro]

La distance AP est minimale lorsque P est le projeté orthogonal de A sur (BC), autrement dit, le pied de la hauteur issue de A dans ABC.

Dans cette configuration, APB est rectangle en P, et tu n'auras pas de difficulté à calculer AP grâce à un peu de trigonométrie de collège!

[Sowsow]

Oui, mais pour prouver que la distance AP est minimale lorsque P est le projeté orthogonal de A sur (BC) ( je suis totalement d'accord ), il me faut bien étudier une fonction, non ? Autrement dit, je ne peux pas l'écrire sans l'avoir au préalable prouvé. Et je bloque justement à ce niveau là :S

[emdro]

C'est très intuitif géométriquement.

Si tu souhaites le démontrer, c'est facile:
En nommant H le pied de la hauteur issue de A dans ABC, et en mettant P quelque part sur (BC), le triangle AHP étant rectangle en H,
d'après Pythagore, AP²=AH²+PH²>=AH²
Donc AP²>=AH et AP>=AH.
La distance AH est donc le minimum possible lorsque P se déplace sur (BC).

[Sowsow]

Eh bien je vous remercie énormément !!
Je vais suivre votre raisonnement !
Je cherchais surement trop compliqué ...
Merci infiniment.
Bonne journée à vous.

[emdro]

Si tu veux absolument le faire analytiquement, tu peux te placer dans un repère orthonormé d'origine A et:
*trouver AC=3
*trouver une équation de (BC):
*Poser x l'abscisse de P, et donc .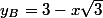
*Tu auras donc les coordonnées de I(x,0) et de .
*Tu peux alors calculer f(x)=IJ² en fonction de x
*tu dérives...

Mais la méthode géométrique est de loin la plus élégante....

[Sowsow]

Merci mais votre première solution me semble la plus appropriée effectivement.
( Pourquoi faire compliquer quand on peut faire simple ? =) ).
Je viens de tout poser sur une feuille, il ne me reste plus qu'à reformuler. D'ailleurs, pour répondre à la question posée dans l'énoncé, après avoir tout démontrer, il me suffit juste de dire qu'il faut placer le point P en H ? Pas besoin de préciser autre chose ?
Je vous remercie encore de votre rapidité et de votre aide.

[emdro]

Non, pas besoin de préciser autre chose: la distance ne peut être inférieure à AH, et comme c'est atteint pour P=H, il suffit de mettre P en H.

Bonne rédaction!