Bonjour a tous,
je suis coince en montrant la proposition suivante:
Si $f$ est une fonction numerique definie sur un ouvert $U$ de $\mathbb{R}$, qui est 2 fois differentiable en $x_0 \in U$, montrer que si $f'(x_0)=0$ et $f''(x_0) < 0$, alors $x_0$ est un maximum local pour f.
Je dois donc trouver une boule de centre $x_0$ et de rayon $\espsilon$ , $B(x_0, \epsilon)$ tel que $f(x) \leq f(x_0)$, pour tout $x \in B(x_0, \epsilon) \cap U$.
J'ai essayer d'utiliser Theoreme des Accroissements finies mais ca ne donne pas ce que j'ai voulu:
f(x)-f(x_0)= f'(c)(x-x_0) avec $c entre $x_0$ et $x$.
et comme $f'(x_0)= 0$, je peux ecrire et appliquer le Theoreme des accroissements finies a $f'$ puisque f esr 2 fois differentiable
$f'(c) = f'(c)-f'(x_0)= f''(d)(c-x_0)$ avec $d$ entre $c$ et $X_0$, donc
$f(x)-f(x_0) = f''(d)(x-x_0)(c-x_0)$ et je suis coince la car je ne peux pas affirmer que $f''(d) < 0$ avec l'hypothese $f''(x_0) < 0$.
J'ai besoin d'indications.
Merci d'avance
Preuve du maximum local
6 messages
- Page 1 sur 1
(Il est nécessaire d'utiliser les balises TEX pour afficher le LaTeX.)
La bonne méthode est l'utilisation d'un développement limité.
Le théorème de Taylor-Young te dit que = f(0) + \frac{f''(0)}{2} x^2 + x^2\varepsilon(x)) (j'ai pris
(j'ai pris 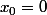 ), avec
), avec  = 0) .
.
C'est à dire = f(0) + \frac{f''(0)}{2} x^2(1 + A\varepsilon(x))) . Comme
. Comme  = 0) , on a bien
, on a bien  \gt 0) sur un voisinage de zéro.
sur un voisinage de zéro.
Ta méthode est plus courte, mais n'est valable que si f est deux fois continument différentiable pas seulement en zéro, mais sur un voisinage de zéro. Le fait que f''(0) < 0 assure alors que cette inégalité est vrai sur tout un voisinage de zéro.
La bonne méthode est l'utilisation d'un développement limité.
Le théorème de Taylor-Young te dit que
C'est à dire
Ta méthode est plus courte, mais n'est valable que si f est deux fois continument différentiable pas seulement en zéro, mais sur un voisinage de zéro. Le fait que f''(0) < 0 assure alors que cette inégalité est vrai sur tout un voisinage de zéro.
Les hypohèses de dérivabilité sont trop faible pour pouvoir utiliser ce théorème, il faut le faire à la main.
Récapitulons les hypothèses : f est définie sur un ouvert de contenant 0. f est continument dérivable sur un voisinage de zéro et f' est dérivable en zéro. De plus, f'(0) = 0, et f''(0) = a < 0.
contenant 0. f est continument dérivable sur un voisinage de zéro et f' est dérivable en zéro. De plus, f'(0) = 0, et f''(0) = a < 0.
Par définition,-f'(0)}{h} = \lim_{h\to 0} \frac{f'(h)}{h}) .
.
En particulier, \sim_{h\to 0} ah) . Comme a est négatif, f' est du signe de l'opposé de h sur un voisinage de zéro. Tu n'as plus qu'à faire un tableau de variation.
. Comme a est négatif, f' est du signe de l'opposé de h sur un voisinage de zéro. Tu n'as plus qu'à faire un tableau de variation.
Récapitulons les hypothèses : f est définie sur un ouvert de
Par définition,
En particulier,
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
