bonjour,
j'ai un exercice où on me dit
la courbe C est définie par:
M(x,y) appartient à C si -x^3+2y^2=1+x-y
Montrer que, cette courbe passe par deux point distincts A et B tous les deux d'abcisse1 . Alors pour ça je remplace x par 1 je trouve équation du second degré que je résous et je trouve les deux points
A(1,1) et B(1,-3/2) Voila pour la première partie pas trop de problème.
Ensuite, je dois calculer le coefficient directeur de la tangente à la courbe en ces deux points mais je n'arrive pas a trouver comment faire.
Fonction implicite
4 messages
- Page 1 sur 1
fonction explicite
bjr,
a-priori, dans un petit voisinage du point A,la formule , donnée par le discriminant
du point A,la formule , donnée par le discriminant  de l'équation du second degré d'inconnue
de l'équation du second degré d'inconnue  est encore valide.
est encore valide.
On est ramené à écrire l'équation d'une tangente d'une courbe avec
avec ) .
.
Même chose au point B avec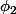 . Avec la formule conjuguée car
. Avec la formule conjuguée car  n'a pas le même signe que
n'a pas le même signe que  .
.
a-priori, dans un petit voisinage
On est ramené à écrire l'équation d'une tangente d'une courbe
Même chose au point B avec
bjr,
l'exercice est un cas particulier facile du théorème des fonction implicites.
Pour comprendre ce qui se passe , prenons l'exemple du cercle unité
du plan euclidien d'origine O et de rayon 1.
C'est l'ensemble des points du plan de coordonnées (x,y) vérifiant:

Ce cercle n'est pas la courbe d'une fonction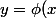)
ni la courbe d'une fonction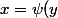)
La raison en est fort simple, pour un x fixé, il y a deux valeurs possibles
pour telles
telles 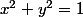 . y n'est donc pas fonction de x.
. y n'est donc pas fonction de x.  n'est pas fonction de y, non plus.
n'est pas fonction de y, non plus.
Maintenant on peut restreindre notre attention au demi-cercle du demi-plan
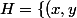 / \quad y \geq 0 \})
Le demi-cercle est alors la courbe caractéristique de la fonction

De même , le demi-cercle situé dans le demi-plan
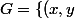 / \quad x \geq 0 \})
est la courbe caractéristique de la fonction:

On obtient un paramètrage local du cercle par la variable y,
le paramètrage étant infiniment dérivable sur l'ouvert
ouvert relatif à l'espace de la deuxième coordonnée.
Le théorème des fonctions implicites développe cette idée dans le cas général.
On a une courbe définie par une relation algébrique
=0) (1)
(1)
ie, le résultat d'un certain calcul algébrique entre coordonnées (x,y)
d'un point de la courbe donne zéro. Evidemment, on peut considérer
des équations algébriques dès que l'on peut faire des calculs, par exemple
dans des anneaux ou des corps finis, sans considération de topologie
de voisinage,etc..
Le thm des fonctions implicites fait le lien avec un autre aspect des courbes:
l'aspect différentiable.
Les courbes peuvent être plus ou moins lisses, admettre des tangentes, ressembler localement à une droite si l'on "zoome".
Ce théorème affirme donc que localement, si la dérivée partielle
de par rapport à y est non nulle, la courbe définie par
par rapport à y est non nulle, la courbe définie par
l'équation (1) se confond avec le graphe d'une fonction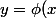) .
.
Le paramètrage est dérivable,
est dérivable, 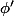
se calcule avec les dérivées partielles de f, et l'on peut récupérer
l'équation d'une droite tangente à la courbe.
Cette équation de tangente est alors une fonction affine habituelle
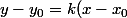)
Le coefficient directeur k se calcule avec les dérivées partielles
de f en)
l'exercice est un cas particulier facile du théorème des fonction implicites.
Pour comprendre ce qui se passe , prenons l'exemple du cercle unité
du plan euclidien d'origine O et de rayon 1.
C'est l'ensemble des points du plan de coordonnées (x,y) vérifiant:
Ce cercle n'est pas la courbe d'une fonction
ni la courbe d'une fonction
La raison en est fort simple, pour un x fixé, il y a deux valeurs possibles
pour
Maintenant on peut restreindre notre attention au demi-cercle du demi-plan
Le demi-cercle est alors la courbe caractéristique de la fonction
De même , le demi-cercle situé dans le demi-plan
est la courbe caractéristique de la fonction:
On obtient un paramètrage local du cercle par la variable y,
le paramètrage étant infiniment dérivable sur l'ouvert
ouvert relatif à l'espace de la deuxième coordonnée.
Le théorème des fonctions implicites développe cette idée dans le cas général.
On a une courbe définie par une relation algébrique
ie, le résultat d'un certain calcul algébrique entre coordonnées (x,y)
d'un point de la courbe donne zéro. Evidemment, on peut considérer
des équations algébriques dès que l'on peut faire des calculs, par exemple
dans des anneaux ou des corps finis, sans considération de topologie
de voisinage,etc..
Le thm des fonctions implicites fait le lien avec un autre aspect des courbes:
l'aspect différentiable.
Les courbes peuvent être plus ou moins lisses, admettre des tangentes, ressembler localement à une droite si l'on "zoome".
Ce théorème affirme donc que localement, si la dérivée partielle
de
l'équation (1) se confond avec le graphe d'une fonction
Le paramètrage
se calcule avec les dérivées partielles de f, et l'on peut récupérer
l'équation d'une droite tangente à la courbe.
Cette équation de tangente est alors une fonction affine habituelle
Le coefficient directeur k se calcule avec les dérivées partielles
de f en
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
