Géo
21 messages
- Page 1 sur 2 - 1, 2
géo
M est un point à la surface de la terre
on dit que sa latitude est de 30°N pour indiquer que EAM=30° (ou a est le centre de la terre) et que M est dans l'hémisphere nord.
on dit que sa latitude est de 30°N pour indiquer que EAM=30° (ou a est le centre de la terre) et que M est dans l'hémisphere nord.
longueur des parallèles
Bonjour,
toutes les mesures d'angles sont en degré.
Dans le triangle HAM, rectangle en H:
)
Longueur du 30° parallèle:
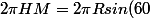 = 2 \pi \times 6370 \frac{\sqrt{3}}{2})
 km
km
longueur du a° parallèle:
du a° parallèle:
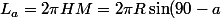)
)
Longueur du 45° parallèle
La formule précédente donne:

J'ai eu la flemme de faire les applications numériques :hum:
Cordialement,
toutes les mesures d'angles sont en degré.
Dans le triangle HAM, rectangle en H:
Longueur du 30° parallèle:
longueur
Longueur du 45° parallèle
La formule précédente donne:
J'ai eu la flemme de faire les applications numériques :hum:
Cordialement,
mathelot a écrit:
Longueur du 30° parallèle:km
tu essayes de comprendre cette formule et puis tu la rentre à la calculatrice.
Le problème, est-ce que tu connais cette valeur remarquable:
Faut considérer un demi-triangle équilatéral de côté 1 pour la démontrer. :zen:
Tu calcule le sinus et le cosinus des angles d'un demi-triangle équilatéral
de côté 1 en le coupant en deux selon une hauteur, et en appliquant le théorème de Pythagore.
ça te donnera les valeurs exactes de sin(30)=cos(60) et sin(60)=cos(30).
la longeur de la 60 ème parallèle
L60= Racine1*pie*6370
=11290.53
est ce que la 60 ème parallèle c bien ca?
en tout cas merci beaucoup de m'avoir aider à comprendr
Comment faire pour calculer la 60àme paralèle merci de m'aider
car je trouve 11290.53
le résultat est donc 20011.94km
ce que j'ai fait puisque j'ai mis une multiplication
je n'arrive pas a y parvenir
L60= Racine1*pie*6370
=11290.53
est ce que la 60 ème parallèle c bien ca?
en tout cas merci beaucoup de m'avoir aider à comprendr
Comment faire pour calculer la 60àme paralèle merci de m'aider
car je trouve 11290.53
le résultat est donc 20011.94km
ce que j'ai fait puisque j'ai mis une multiplication
je n'arrive pas a y parvenir
--------------------------------------------------------------------------------
la longeur de la 60 ème parallèle
L60= Racine1*pie*6370
=11290.53
est ce que la 60 ème parallèle c bien ca?
Comment faire pour calculer la 60àme paralèle merci de m'aider
car je trouve 11290.53
le résultat est donc 20011.94km
ce que j'ai fait puisque j'ai mis une multiplication
avec le calcule avec les cosinus je trouve un autre résultats
pouriez vous me montrer comment vous faite en détaillant merci
la longeur de la 60 ème parallèle
L60= Racine1*pie*6370
=11290.53
est ce que la 60 ème parallèle c bien ca?
Comment faire pour calculer la 60àme paralèle merci de m'aider
car je trouve 11290.53
le résultat est donc 20011.94km
ce que j'ai fait puisque j'ai mis une multiplication
avec le calcule avec les cosinus je trouve un autre résultats
pouriez vous me montrer comment vous faite en détaillant merci
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

