3=0

[Hyp]

@ Imod: Oui erreur de ma part. Je voulais dire que l'on pouvait obtenir l'équivalence en expulsant le cas de x nul, et non pas -forcément- l'implication.

[bitonio]

On retrouve au passage un des principes de résolutions des équations: on travaille en implications et à la fin on fait une synthèse pour voir lesquels des solutions potentielles marchent.

[Imod]

Une règle simple , quand on est en mode "calcul" , on est plus con qu'une calculatrice . Les calculs finis , on redevient soi-même et on met un petit coup de balai et tout rentre dans l'ordre . C'est comme ça que je fonctionne .

Imod

[bitonio]

Une règle simple , quand on est en mode "calcul" , on est plus con qu'une calculatrice . Les calculs finis , on redevient soi-même et on met un petit coup de balai et tout rentre dans l'ordre . C'est comme ça que je fonctionne .

Imod

Enigme de la semaine, comprendre la phrase de Imod :we:

[Patastronch]

Enigme de la semaine, comprendre la phrase de Imod :we:

Ben il dit qu'il faut se relire quand on est dans une phase calculatoire, c est tout. J'ai gagné un truc ?

[bitonio]

Ben il dit qu'il faut se relire quand on est dans une phase calculatoire, c est tout. J'ai gagné un truc ?

Ma reconnaissance éternelle Je vois pas le rapport avec le balais mais c'est pas grave!

[Imod]

Ma reconnaissance éternelle Je vois pas le rapport avec le balais mais c'est pas grave!

Quand on raisonne par implication on génère des déchets de toutes sortes qu'il faut ensuite enlever , suis-je opaque à ce point ?

Imod

[bitonio]

Quand on raisonne par implication on génère des déchets de toutes sortes qu'il faut ensuite enlever , suis-je opaque à ce point ?

Imod

Ah je comprends enfin. Je dois pas être assez aware...

[mathk]

Soit x un réel tel que x²+x+1=0
alors on a x+1=-x²
mais aussi x(x+1)+1=0 en remplaçant on obtient x(-x²)+1=0 c'est à dire
et donc x=1 et 1+1+1=0
:hein:

Peut tu reposer ta demonstration pour que je comprenne quand est ce que tu a utilise l'equivalence au lieu de l'implication.
Thx

[Patastronch]

Peut tu reposer ta demonstration pour que je comprenne quand est ce que tu a utilise l'equivalence au lieu de l'implication.
Thx

On a
x²+x+1=0 => x^3=1
mais pas x^3=1 => x²+x+1=0

L'endroit precis c 'est au moment ou il dit on remplace.

[mathk]

On a
x²+x+1=0 => x^3=1
mais pas x^3=1 => x²+x+1=0

L'endroit precis c 'est au moment ou il dit on remplace.

D'accord merci

Donc pour etre rigoureux
On a

x(x+1) +1 = 0
-x²=x+1

=> x^3=1 et pas
Mais question bete pourquoi? J'arrive pasa saisir la logique.
En gros comment je fait pour savoir quand je dois mettre et quand je peut mettre que =>.

Je me souviens de l'avoir appris mais je me rappelle plus.
Merci

[Imod]

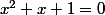
Deux équations sont équivalentes si elles ont les mêmes solutions . Il est clair que et ne sont pas équivalentes car 1 est solution de la première mais pas de la 2ème .

Imod

[mathk]

Je pense me souvenir d'un explication plus rigoureuse mais je ne suis pas sur de ca justesse:

Ceci peut se comprendre si on definit le domaine d'application des equations:

x² + x + 1 = 0 est definit dans C - IR
tand dit que:
x^3=1 est definit dans C.

pour etablire une equivalance il faut alors choisir le plus petit ensemble de definition commun des 2 equations.

Soit [(C-IR) intersection C] cad (C - IR)

Ont peut donc parfaitement affirmer que:

x²+x+1=0 <=> x^3=1 dans (C-IR)

[mathk]

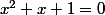
Deux équations sont équivalentes si elles ont les mêmes solutions . Il est clair que et ne sont pas équivalentes car 1 est solution de la première mais pas de la 2ème .

Imod

Ceci peut parfois ne pas etre juste dans le cas ou l'on c'est tronpe

[moutonjr]

en fait en récapitulant enfin :
x²+x+1 n'a de solution uniquement dans les Complexes.soit.
si z appartenant à C résout :
z²+z+1 = 0
et donc avec la double implication on obtient :
z^3 = 1
On obtient les deux solutions de départ,
(-1±i;)3)/2 et une valeur créée par inclusion : 1

tel x = 1
<=> x² = 1
<=> x = ±;)1 = ±1 <=> 1= -1
-1 est ici créée par inclusion.
Ici c'est pareil.

[Flodelarab]

J'adore les fausses démonstration et je suis content de tomber sur cette discussion. Je ne connaissais pas celle-là. Passionnant :lol: