Probabilités : un probleme d'urnes
15 messages
- Page 1 sur 1
Probabilités : un probleme d'urnes
Bonjour à tous !
Encore un probleme de proba ou je bloque...(et ce ne sera surment pas le dernier !)
On dispose de N+1 urnes numérotées de 0 à N.
L'urne numéro k contient k boules rouges et (N-k) boules noires.
On tire une des urnes avec équiprobabilité, puis on procède avec cette urne à une série de n tirages avec remise.
a) Calculer la probabilité d'avoir choisi l'urne n°1 sachant qu'on a tiré n boules rouges.
b) Calculer la probabilité de tirer n boules rouges.
c) Calculer la probabilité de tirer une boule rouge au tirage (n+1)sachant qu'on a déja tire n boules rouges.
d) Determiné les limites des probabilités précédentes quand N tend vers l'infini.
Je suppose que pour la question a), il faut utiliser la formule P(B|A) = P(B"inter"A) / P(A) , mais dans ce cas j'utilise deja la reponse à la question b) !!
Bref, je ne vois pas vraiment comment m'y prendre....
Encore un probleme de proba ou je bloque...(et ce ne sera surment pas le dernier !)
On dispose de N+1 urnes numérotées de 0 à N.
L'urne numéro k contient k boules rouges et (N-k) boules noires.
On tire une des urnes avec équiprobabilité, puis on procède avec cette urne à une série de n tirages avec remise.
a) Calculer la probabilité d'avoir choisi l'urne n°1 sachant qu'on a tiré n boules rouges.
b) Calculer la probabilité de tirer n boules rouges.
c) Calculer la probabilité de tirer une boule rouge au tirage (n+1)sachant qu'on a déja tire n boules rouges.
d) Determiné les limites des probabilités précédentes quand N tend vers l'infini.
Je suppose que pour la question a), il faut utiliser la formule P(B|A) = P(B"inter"A) / P(A) , mais dans ce cas j'utilise deja la reponse à la question b) !!
Bref, je ne vois pas vraiment comment m'y prendre....
J'ai beau chercher, ... je crois que mon probleme est dans la compréhension des questions !!
Pour la question a), j'ai nommé deux evenement :
A : "on tire n boules rouges"
B : "on a choisi l'urne n°1"
Ensuite, je trouve P(a"inter"B) = (1/N)^n (car il n'y a qu'une seule boule rouge dans l'urne n°1, et qu'on fait n tirages avec remise.
Pour P(A), je trouve (k/N)^n, car pour une urne quelconque, il y a k boules rouges.
ainsi, je trouve P(B|A) = (1/k)^n
Pour la question b), je pensais à faire le produit de k=0 à k=N de (k/N)^n....
Pour les questions c) et d), je ne vois pas du tout comment faire...
Merci à ceux qui pourront me donner un petit coup de pouce !!
Pour la question a), j'ai nommé deux evenement :
A : "on tire n boules rouges"
B : "on a choisi l'urne n°1"
Ensuite, je trouve P(a"inter"B) = (1/N)^n (car il n'y a qu'une seule boule rouge dans l'urne n°1, et qu'on fait n tirages avec remise.
Pour P(A), je trouve (k/N)^n, car pour une urne quelconque, il y a k boules rouges.
ainsi, je trouve P(B|A) = (1/k)^n
Pour la question b), je pensais à faire le produit de k=0 à k=N de (k/N)^n....
Pour les questions c) et d), je ne vois pas du tout comment faire...
Merci à ceux qui pourront me donner un petit coup de pouce !!
Cachou-doo a écrit:
Pour la question a), j'ai nommé deux evenement :
A : "on tire n boules rouges"
B : "on a choisi l'urne n°1"
Ensuite, je trouve P(a"inter"B) = (1/N)^n (car il n'y a qu'une seule boule rouge dans l'urne n°1, et qu'on fait n tirages avec remise.
Pour P(A), je trouve (k/N)^n, car pour une urne quelconque, il y a k boules rouges.
ainsi, je trouve P(B|A) = (1/k)^n
c'est bizarre que ton résultat dépende de k, non ?
A mon avis P(A) ne doit pas dépendre de k et c'est là que je j'arrive pas
pour la a), je pense qu'il faut déjà calculer le nombre total de boule rouge
c'est à dire}{2})
dans l'urne 1 il y a une rouge donc la proba de tombé sur celle là est de}{2}}= \frac{2}{N(N+1)})
puis après on refait ça n fois donc là je mettrais à la puissance n et on trouve (peut-être) la proba d'avoir choisit l'urne numéro 1 en ayant tiré n boules rouges cad :
}\)^n)
si N=1 la proba est bien de 1 et si N tend vers l'infini la proba va vers 0. Bon si N=0 ça marche pas très bien mais en même temps dans ce cas l'urne 1 n'existe pas...
Je suis quand même pas très sûre.
>
c'est à dire
dans l'urne 1 il y a une rouge donc la proba de tombé sur celle là est de
puis après on refait ça n fois donc là je mettrais à la puissance n et on trouve (peut-être) la proba d'avoir choisit l'urne numéro 1 en ayant tiré n boules rouges cad :
si N=1 la proba est bien de 1 et si N tend vers l'infini la proba va vers 0. Bon si N=0 ça marche pas très bien mais en même temps dans ce cas l'urne 1 n'existe pas...
Je suis quand même pas très sûre.
>
Bonne idée de calculer le nombre de boules rouges total ! je N'y avais même pas pensé...
Moi je calcule la probabilité de tirer n boules rouges dans l'urne n°1. Comme il n'y a qu'une seule bouge rouge dans cette urne et que l'on fait un tirage avec remise, et je trouve P=(1/N)^n
Ensuite, je calcule la probabilité de tirer n boules rouges parmis toutes les boules rouges : P'=(N(N+1)/2N^n)^n, puisqu'on fait des tirages avec remises.
(nombres de cas favorables sur nombres de cas possibles, le tout à la puissance n pour les n tirages)
Enfin, je fais le quotient de P par P', et je trouve P("avoir choisi l'urne n°1 sachant qu'on a tiré n boules rouges") = (2N^(n-2)/N+1)^n
je ne suis pas sure non plus de mon resultat...mais si N=1 la proba est aussi de 1, et si N=0, la proba est de 0
Moi je calcule la probabilité de tirer n boules rouges dans l'urne n°1. Comme il n'y a qu'une seule bouge rouge dans cette urne et que l'on fait un tirage avec remise, et je trouve P=(1/N)^n
Ensuite, je calcule la probabilité de tirer n boules rouges parmis toutes les boules rouges : P'=(N(N+1)/2N^n)^n, puisqu'on fait des tirages avec remises.
(nombres de cas favorables sur nombres de cas possibles, le tout à la puissance n pour les n tirages)
Enfin, je fais le quotient de P par P', et je trouve P("avoir choisi l'urne n°1 sachant qu'on a tiré n boules rouges") = (2N^(n-2)/N+1)^n
je ne suis pas sure non plus de mon resultat...mais si N=1 la proba est aussi de 1, et si N=0, la proba est de 0
Salut,
la question a) est en effet bizarre. Je me demande si il ne s'agit pas plutôt de calculer la proba de tirer n boules rouges sachant que l'on a choisi l'urne 1.
Pour la question b) on calcule la proba de tirer n boules rouges sachant que l'on a choisi l'urne k.
Elle est égale à}^n) .
.
La proba de l'évènement :> est donc}^n)
Les évènements > forment un système exhaustif.
forment un système exhaustif.
La proba de tirer n rouges est donc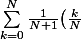}^n} \,=\,\frac1{(N+1)N^n}\sum_{k=1}^N {\,k^n})
On peut alors répondre à la question a)
la question a) est en effet bizarre. Je me demande si il ne s'agit pas plutôt de calculer la proba de tirer n boules rouges sachant que l'on a choisi l'urne 1.
Pour la question b) on calcule la proba de tirer n boules rouges sachant que l'on a choisi l'urne k.
Elle est égale à
La proba de l'évènement :> est donc
Les évènements >
La proba de tirer n rouges est donc
On peut alors répondre à la question a)
nuage a écrit:Salut,
la question a) est en effet bizarre. Je me demande si il ne s'agit pas plutôt de calculer la proba de tirer n boules rouges sachant que l'on a choisi l'urne 1.
oui mais à ce moment là si on fait la même chose avec l'urne N, on aura la proba de tirer n boules rouges sachant que l'on a choisi l'urne N et ça c'est égal à 1.
Je suis d'accord avec ta proba de tiré n rouges, mais quand je fais
A : proba d'avoir choisit l'urne 1
B : proba de tiré n rouge
et comme tu l'as dis
donc :
et si je me suis pas trompé en prenant N=1 ça fait 2
:cry2:
mais je sais pas si on peut utiliser cette formule
et il est moche mon inter comment on peut le faire plus petit ?
Salut,
avec tes notations on a=P(B|A)\times P(B) =\frac1{(N+1)N^n}) d'où
d'où
=\frac{1}{\sum_{k=1}^N k^n})
Et, bien entendu, si il y a seulement une urne avec une boule blanche et une urne avec une boule rouge la proba d'avoir pris l'urne 1 sachant qu'on a tiré une (ou plus) boule rouge est 1.
Une remarque sur les limites demandées à la fin : on peut penser à des sommes de Riemann.
avec tes notations on a
Et, bien entendu, si il y a seulement une urne avec une boule blanche et une urne avec une boule rouge la proba d'avoir pris l'urne 1 sachant qu'on a tiré une (ou plus) boule rouge est 1.
Une remarque sur les limites demandées à la fin : on peut penser à des sommes de Riemann.
nuage a écrit:Salut,
avec tes notations on ad'où
Et, bien entendu, si il y a seulement une urne avec une boule blanche et une urne avec une boule rouge la proba d'avoir pris l'urne 1 sachant qu'on a tiré une (ou plus) boule rouge est 1.
Une remarque sur les limites demandées à la fin : on peut penser à des sommes de Riemann.
oui d'accord mon
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
