Bonsoir :happy3:
Une preuve entièrement géométrique :
L'équation se ramène à
^{n}=1)
ie
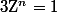
avec

Les Z sont situés sur le cercle unité.
Or

équivaut à

Il suffit donc de chercher l'image du cercle unité par l'homographie

Un calcul rapide nous donne que
=b-(a+b)\times \bar{\frac{1}{\bar{z-1}}})
D'où
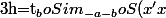oI_{O,1}ot_{-1})
Tout va se jouer sur la première translation

. Elle va envoyer le cercle unité sur un cercle passant par O.
Son image par l'inversion I(O,1) est une droite.
La symétrie S va envoyer cette droite sur une autre droite, pareil pour la similitude et pour la translation.
Au final h envoie le cercle unité sur une droite. CQFD.
:happy3:
