Exo fonction 1S

[Magalie0011]

Bonjour,

J'ai un exo super court, mais je sais pas par où commencer. Pouvez vous m'aider svp?

Voici l'énoncé :

f est la fonction définie sur R par :
f(x) = x^3 -3x² + 7

Déterminez le plus petit entier relatif m, tel que, pour tout x réel, si x >= m alors f(x) >= 10

Voilà, merci de votre aide.

[stoomer]

étudies la fonction g(x) = f(x) - 10

[Magalie0011]

g (x) = f(x) - 10
= x^3 - 3x² - 3
= x^3 -3 (x² + 1)

voilà.

[stoomer]

non il faut l'étudier c'est à dire dérivée tableau de variation et tu cherches x pour que g(x) soit positive ça devrait répondre à ta question
désolé je dois partir
@++

[Magalie0011]

alors g'(x) = 3x² - 6x
delta = 36
x1 = 0
x2 = 2

g'(x) : positif de - l'infinie à 0 ; negatif de 0 à 2 ; positif de 2 à + l'infinie
g(x) = croissant decroissant croissant

g(0) = - 3
g(2) = -7

donc m = -7

c'est bien sa?

[Sa Majesté]

alors g'(x) = 3x² - 6x
delta = 36

Mon prof de maths (celui-là même qui m'appelait Sa Majesté) t'aurait rangée parmi ce qu'il appelait les "ayatollahs du discriminant"
Franchement 3x² - 6x = 3x (x - 2) non ?
On utilise le discriminant quand il n'y a pas de solution évidente

[Noemi]

Il faut chercher la valeur de x telle que g(x) = 0

[Magalie0011]

ah oui. :marteau: j'avais pas vu. mais le résultat est le meme non?
c'est juste la reponse sinon par rapport à l'exo?

[stoomer]

non tu n'as pas encore trouvé m!!
il faut que tu regardes dans ton tableau de variation quand g(x) est positive ou nulle!!

[Magalie0011]

alors, sur mon tableau de variation, la courbe doit passer par 0 ente 2 et + l'infinie. mais est ce que je dois rajouter l'antésédent pour lequelle son image est égale à 0. commen je fais?

[stoomer]

t'as du certainement voir le théorème des valeurs intermédiaires non?

[Magalie0011]

euh non. mais comment il faut faire?

[stoomer]

il va falloir que tu trouves par tatonnement le plus petit x tel que g(x) = 0

[La Boule]

Si m est un entier alors en utilisant la bijection ( théorème des valeurs intermédiaires comme l'as dit stoomer ) tu calcules f(3), f(4) et tu vas remarquer quelque chose. Le fait que m soit entier simplifie grandement les choses !

[stoomer]

d'où m = 4 .... bonne soirée!

[Magalie0011]

alors j'ai cherché avec ma calculette graphique, et c'est comprit entre 3,2 et 3,3.
Commen je fais maintenant?

[La Boule]

Mais si tu veux une inégalité alors puisque f(3) négatif et f(4) positif alors

x STRICTEMENT supérieur a 3 ou mathématiquement parlant :

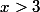
[stoomer]

mais comme on veut x supérieur ou égal à m (m entier) pour que f(x) soit supérieure ou égale à 10 alors on prendra m = 4 ....

[Magalie0011]

dacord je vous remercie beaucoup. bonsoir.

[La Boule]

mais comme on veut x supérieur ou égal à m (m entier) pour que f(x) soit supérieure ou égale à 10 alors on prendra m = 4 ....

On est d'accord mais on lui demande d'écrire son résultat sous la forme
et pas on raisonne sur un intervalle pas sur une valeur. Parce que f(5) > 10, f(6)> 10 etc.