Développement limité

[georgess]

Bonsoir , supposez que vous connaissez le développement limité d'une fonction , comment vous faites pour calculer le développement limité de sa fonction réciproque ?

merci

[Nightmare]

Bonsoir :happy3:

Si ta fonction et sa réciproque sont n fois dérivables alors on peut y aller à coup de Taylor.

Sinon dans tout les cas, on revient à la définition de la réciproque, à savoir que fof^-1 donne l'identité.

[busard_des_roseaux]

Bonjour,

on connait le DL ou le DSE de f au voisinage de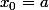
on écrit le développement de g au voisinage de
avec des coefficients inconnus ,
on écrit le Dl ou le DSE de gof(x)=x en composant f et g.
on identifie les DL, ce qui donne des relations pour calculer
les coeff. inconnus.


exemple:

connu

inconnu

On compose les deux. on identifie à x=0+1.x+0+.. en vertu de l'unicité.

[georgess]

ok mais alors j'utilise la formule de taylor-young ou taylor lagrange ?

[Nightmare]

D'après toi pour un DL ?

[busard_des_roseaux]

ok mais alors j'utilise la formule de taylor-young ou taylor lagrange ?

peu importe. ce qui compte, c'est la composition des deux DL et l'unicité
des coefficients. On trouve des conditions nécéssaires.

Pour la suffisance, on a le théorème d'inversion locale qui dit que si est non nul et f k fois continuement dérivable, est aussi de classe Ck.

[georgess]

je dirai young car c'est pour un DL en un point , lagrange c'est pour in intervalle ?

[Nightmare]

Lagrange ça ne te donne pas un réel mais une valeur exacte en un point (même s'il y a un c inconnu). Bien sûr on peut s'arranger pour encadrer le reste de Lagrange et obtenir un DL mais autant y aller directement par la formule de Young qui te dit que ton reste de Lagrange est un petit o.

[georgess]

ok alors laissez moi 2min je cherche le DL de arctan en 0 à l'ordre 5 , je le calcule et j'envois ça .

[georgess]

ya un truc qui va pas , si je cherche un DL en 0 , la formule de young commence par :

f(x) = f(a) + (x-a)f'(a)+...le 0 c'est le a ou le x ?

[Nightmare]

Oula, il faut reprendre toutes les bases des DL là...

Qu'est-ce qu'un DL ? C'est l'approximation d'une fonction au voisinage d'un point ou d'un nombre?

Si tu remplaces x par 0, t'approches un nombre ou une fonction?
Et si tu remplaces a par 0?

[georgess]

si je remplace x par 0 j'approche un nombre , si je remplace a par 0 j'approche une fonction , c'est mon avis je me trompe peut etre .

désolé j'ai les cours les plus merdiques de france sur les DL et pourtant l'université est censé etre au top en maths .

[atito]

si je remplace x par 0 j'approche un nombre , si je remplace a par 0 j'approche une fonction , c'est mon avis je me trompe peut etre .

désolé j'ai les cours les plus merdiques de france sur les DL et pourtant l'université est censé etre au top en maths .

Je me permet de m'incruster un peu.

On prend l'habitude de noté x la variable. ici x varie dans un voisinage de a.
le but du DL est d'écrire f(x) sous forme d'un polynôme au voisinage d'un point a. le 0 est donc a.

[Nightmare]

Oui c'est bien ça (concernant les DL, pour ton université je n'en sais rien :lol3: )

Bref l'idée d'un DL est donc d'approcher une fonction au voisinage d'un point par un polynôme.

La formule de Taylor-Young te dit que pour une fonction n fois dérivables, alors au voisinage de a, f(x) s'approche par
En fait elle te dit que f est exactement égal à ce polynôme plus un truc négligeable devant (x-a)^n (notre petit o)

En particulier en 0, on a

[georgess]

ok alors le DL d'ordre 5 de la fonction arctan c'est :

1 + x/1+x² + x/2 * ln(1+x²) + x³/3! * 2x/(1+x) + x^4/4 2/(1+x²) + x^5/5! * 2ln(1+x)²

[atito]

ok alors le DL d'ordre 5 de la fonction arctan c'est :

1 + x/1+x² + x/2 * ln(1+x²) + x³/3! * 2x/(1+x) + x^4/4 2/(1+x²) + x^5/5! * 2ln(1+x)²

arctan(0) = ?

[Nightmare]

C'est un polynôme ton truc à droite là ?

[georgess]

arctan(0) = 0 désolé je me suis trompé , mon truc à droite ne ressemble pas bcp à un polynome mais j'ai appliqué young ...

[leon1789]

si je remplace x par 0 j'approche un nombre , si je remplace a par 0 j'approche une fonction , c'est mon avis je me trompe peut etre .

C'est une vision de la chose...

désolé j'ai les cours les plus merdiques de france sur les DL

A mon avis, ce n'est pas une question de cours ! Mais c'est plus un problème de grosses lacunes en ce qui te concerne : il n'y a qu'à lire tous tes messages pour s'en convaincre.

et pourtant l'université est censé etre au top en maths .

Le problème de l'université, c'est de faire faire des maths à des étudiants qui ne sont visiblement pas fait pour ça...

Désolé d'avoir un ton très grave (je vais tuer l'ambiance là...), mais remettre en cause les compétences de tes enseignants alors tu ne comprends pas grand chose en trigo, en algèbre, et analyse, etc., c'est un peu fort.

Je remarque que tu essaies de comprendre grâce au forum : est-ce que cela te fais réellement comprendre, ou bien cela te permet juste d'en avoir l'impression ? Est-ce que tu n'aurais pas la possibilité d'avoir une méthode de travail plus efficace que de passer des heures à essayer de trouver sur le forum de quoi répondre aux questions des tes exos ? Qu'en penses-tu ?

[georgess]

leon sache une chose : etre prof est quelquechose , etre bon pédagogue en est une autre .