Une simple démo

par **toto_tom** » 16 Fév 2008, 21:00

Bonsoir. Je fais appel à vous car on me demande une démonstration mais je n'arrive pas du tout à le faire. Voici l'unique énoncé :

Montrer que la suite (Un) définie par Un=(-1)^n est divergente.

Merci d'avance. Faut-il le faire par l'absurde?

par **Huppasacee** » 16 Fév 2008, 21:46

Bonsoir

Par l'absurde est une bonne voie

par **Nightmare** » 16 Fév 2008, 22:42

Bonsoir :happy3:

L'idée est de dire que si la suite convergeait disons vers l, tous les termes de la suite serait dans une même boite contenant l à partir d'un certain rang. Sauf que si on est un peu malin, il est facile de construire une boite qui ne va pas contenir 1 et -1 en même temps ce qui conduit à une absurdité puisque la suite ne prend que ces deux valeurs.

Plus rigoureusement, on fixe epsilon positif tel que à partir d'un certain rang N,

Prenons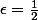

On aurait donc qu'à partir d'un certain rang n,

C'est embêtant car l est forcément dans [-1;1].
S'il est dans [0;1] alors on aura

à partir d'un certain rang N: Absurde car u(n) va prendre la valeur -1 soit en N, soit en N+1

S'il est dans [-1;0] c'est la même rengaine avec l+1/2.
Dans tous les cas on obtient une absurdité. La suite ne peut donc pas converger. Puisqu'elle ne peut pas aller vers l'infini, elle n'admet pas de limite.

Sinon on sort l'artillerie lourde mais ce n'est pas de niveau lycée :
Si (Un) convergeait alors (U(2n)) et (U(2n+1)) convergerait vers la même limite. Absurde car ces deux suites sont constantes respectivement égales à 1 et -1.

:happy3:

par **toto_tom** » 16 Fév 2008, 22:45

Voilà ce que j'ai essayé.

(Un) converge vers l, donc il existe p tel que pour tout n>p, Un appartient à ]l-r;l+r[.

Or si n>p avec p=2n+1

(-1)^n < (-1)^(2n+1) donc on a l'absurdité. Mais en revanche pour p=2n, (-1)^n=(-1)^2n alors comment je fais? La rédaction est-elle rigoureuse?

par **toto_tom** » 16 Fév 2008, 22:53

Ok j'ai posté en même temps que vous!

Dans [1;0] -1/2 < l + 1/2 < Un c'est ça? je suis pas sûr d'avoir saisi cette partie

la méthode artillerie lourde va plus dans le même sens que ce que j'ai fait, sauf que j'ai du mal à comprendre votre justification

par **Nightmare** » 16 Fév 2008, 22:54

Qu'est-ce que tu n'as pas compris dans la première preuve?

La deuxième est simple.

(U2n) converge vers 1 et (U2n+1) converge vers -1

Or Si (Un) convergeait, ces deux suites auraient la même limite => Contradiction.

par **toto_tom** » 16 Fév 2008, 22:54

AH non en fait, j'ai même très bien compris l'artillerie lourde lol c'est plus simple

par **toto_tom** » 16 Fév 2008, 22:55

Oui oui la 2e est plus simple!
Merci de ton aide en tout cas, c'est sympa d'aider de jeunes lycéens!

par **Nightmare** » 16 Fév 2008, 22:58

Cela dit l'artillerie lourde n'est pas de niveau lycée (sauf si tu l'as vu en cours).

Je t'en prie en tout cas.

:happy3:

Une simple démo

Une simple démo

Qui est en ligne