Equation differentielle

[georgess]

Bonsoir à tous , j'ai l'exercice suivant :

Résoudre sur ]0;pi[ l'équation différentielle d'inconnue y(x) :

sin(x) y'(x) - cos(x) y(x) = 1 .

1) calculer la dérivée de cotg(x) = cos(x)/sin(x) .

Je sais pas ce que veut dire "cotg" mais voici le résultat pour ma dérivée :

(-sin(x) - cos²(x)) / (sin²x) .

Jusque là vous etes d'accord ? :happy2:

merci de votre aide .

[Elvix]

oui... bravo! :++:

(cotg = "cotangente" = 1/tangente)

[Moka]

Salut,

pour l'équa diff je peux pas trop t'aider j'ai un peu de mal avec sa ^^

sinon cotg c'est la co tangente =1/tg donc cos/sin

c'est tout sur quoi je peux t'aider ^^

[georgess]

ok , bon c'etait pas bien difficile elvix je prends ton bravo avec ironie lol , seconde question :

2) Résoudre l'équation homogène associée sin(x) y'(x) - cos(x)y(x) = 0 .

Je la réécris comme celà :

y'(x)/y(x) = cos(x)/sin(x) , donc j'ai :

ln(y(x)) = A(x) + C , C est une constante et A une primitive de la fonction cotg .

Je connais la primitive de la fonction tangente mais pas sa primitive inverse , ya une façon pour la calculer ?

[Nightmare]

Bonsoir,

Allons, cos/sin c'est du type u'/u non?

[georgess]

mais bien sur j'avais oublié lol , donc facile c'est :

ln y(x) = sin(x) , la solution de l'equation homogène est sin(x) .

3) en déduire la solution générale de l'équation différentielle .

Là je dois chercher une solution particulière non ?

[georgess]

mais bien sur j'avais oublié lol , donc facile c'est :

ln y(x) = sin(x) , la solution de l'equation homogène est sin(x) .

3) en déduire la solution générale de l'équation différentielle .


là je dois chercher une solution particulière non ?

[Elvix]

Et ta constante C, elle a disparu au passage?
Ensuite, tu peux trouver une solution particulière ou faire la méthode de la "variation de la constante" (c'est rigolo une constante qui varie, non?)

[georgess]

j'ai une petite question avant : ma solution homogène est de la forme K e^(A(x) , moi j'ai trouvé sin(x) + C , alors ici où est le e , le A(x)...

le A(x) c'est mon sin(x) je suppose mais le C où il se retrouve ?

[georgess]

nan c'est bon j'ai compris par contre pour la méthode de la variation de la constante je sais pas par quelle équation démarrer mes cours sont trop formels et on y comprend rien , de quelle équation dois je partir ?

[Elvix]

Et bien, tu as une solution de l'équation homogène:
f(x)=Ksin(x)
La variation de la constante consiste à chercher une solution sous la forme
f(x)=K(x)sin(x) où K est la fonction que l'on va essayer de trouver.

Tu injectes tout ça dans ton équation de départ, et des miracles vont se produire...

[georgess]

equation de départ :

sin(x)y'(x) - cos(x)y(x) = 1

Je remplace y par K(x) sin(x) :

sin(x) K'(x) sin(x) + K(x) cos(x) - cos(x) K(x) sin(x) = 1 .

Je ne vois pas de miracle en ce qui me concerne...

meme en réduisant :

sin²K'(x) + K(x) cos(x) [ sin x + 1] = 1

[Elvix]

Tu t'es planté en dérivant :langue2: . Tu as oublié le sin(x) en facteur

[georgess]

j'ai oublié une paranthèse oui :

sin(x) [K'(x)sin(x) + K(x)cos(x)] - cos(x)[K(x)sin(x)] = 1

je vois pas de miracle en tout cas...

[georgess]

ah si attends

[nuage]

Salut,
pour la méthode de la variation de constante :
Tu as trouvé que les solutions de l'équation homogène sont de la forme .
Tu prends k fonction de x.
L'équation devient
d'où
raison pour la quelle on t'a fait calculer la dérivée de .
Tu en déduit facilement que
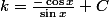
Puis que

[georgess]

voilà en réduisant j'ai donc sin²x K'(x) = 1

K'(x) = 1 /sin² x , mais après je vois pas en quoi ça me donne la solution générale de l'équation meme en calculant la primitive

[Elvix]

C'est bien ça nuage. Bravo. Et pédagogue en plus!

Pour en revenir à notre problème:
tu vas être capable de trouver K(x) en t'aidant de la première question.
Et ensuite... c'est fini: f(x)=K(x)sin(x).

[georgess]

nuage désolé mais je vois pas du tout le rapport avec la dérivée du départ...

[Elvix]

cos² +sin²=...