Fonction exponentielle

[coco]

Bonjour à tous, est ce que quelqu'un pourrait m'aider s'il vous plaît?
Voici mon énoncé:

Soit la fonction f définie sur R par:
f(x)=e^-x (cosx + sinx)

1) a) Exprimer sin(x+pi/4) en fonction de sin x et cos x. (jusque là pas de problème, je me suis servi de:sin(a+b)=sina cosb + sinb cosa et je suis arrivé à sin(x+pi/4)= sin x cos pi/4 + sin pi/4 cos x)

En déduire que pour tout réel x, on a:
f(x)=(racine de 2) e(^-x) sin (x+pi/4)
(pas de problème, je me sert du résultat trouvé ci dessus)

Par contre pour la suite je suis perdu:

b) Résoudre dans R l'équation f(x)=0

c)Justifier que la limite de f en + infini est 0 (cette question je crois que j'y arriverait mais seulement je ne trouve pas f(x)=0)

2) On désigne par f' la fonction dérivée de f sur R

a) Démontrer que, pour tout nombre réel x: f'(x)=-2e(^-x) sin x
(pas de problème pour cette question)

b) Résoudre dans R l'équation f'(x)=0

3) On note I l'intrevalle [-pi/4; 7pi/4]

a) Etudier le signe de f'(x) sur l'intervalle I et dresser le tableau de variation de f sur I.

Merci beaucoup de m'aider car je bloque sur quelques questions.

[coco]

personne ne peut m'aider?

[becirj]

La trigonométrie semble te poser quelques problèmes.
1.b) La fonction exp n'est jamais nulle donc f(x)=0 lorsque
Le sinus est nul pour tous les réels de la forme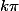 avec 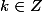. De ceci on déduit les solutions de l'équation.

c) Attention, la question est délicate car la fonction sinus n'a pas de limite en , il faut donc procéder par encadrement.
sin est encadré par -1 et 1. On en déduit un encadrement de f(x) qui permet de trouver la limite.

2.b) Voir 1.b)

3.a) f'(x) a le signe contraire de sin x. Utilise le cercle trigonométrique en en faisant le tour de à pour bien voir le signe de sin x.

[JeePs]

Salut!
b) Comme pour tout réel x, e^(-x) est différent de 0, l'équation f(x)=0 équivaut à: sin(x+pi/4)=0 ou x+pi/4=0 [pi]
Donc l'ensemble des solutions de cette équation s'écrit {(kpi-pi/4) /k appartient à Z}

c) t as pas besoin d avoir répondu à la question b) pour faire celle ci:
Comme lim e^(-x)=0 en + l'infini et que pour tout réel x, -1<=sin(x+pi/4)<=1
tu as directement que f a pour limite 0 en + l'infini.

2) b) Comme précédemment f'(x)=0 <=> sinx=0 <=> x=0[pi]
Donc cette eq admet pour ensemble de sols: {kpi / k appartient à Z}

3) pour tout x de I, -2e^(-x)<0
Pour x de [-pi/4,0], sinx<=0 donc f'(x)>=0
Pour x de [0,pi], sinx>=0 donc f'(x)<=0
Enfin pour x de [pi,7pi/4], sinx<=0 donc f'(x)>=0
f'(x) s'annule pour x=0 ou x=pi
Tu devrais pas avoir de mal à en déduire les variations de f
Voilà @++ :zen:

[coco]

Merci beaucoup