Calcul de dérivée, formule de Leibniz ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hmida
- Messages: 5
- Enregistré le: 14 Nov 2007, 14:29
-
 par Hmida » 04 Fév 2008, 19:37
par Hmida » 04 Fév 2008, 19:37
Bonjour,
pour calculer la dérivée n-ème de exp(x)sinx, j'utilise la formule de Leibniz.
J'aboutis à exp(x).(somme de k=0 à n)(k parmi n).sin(x+kpi/2)... comment avancer ? Merci pour votre aide !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Fév 2008, 19:38
par Nightmare » 04 Fév 2008, 19:38
Bonsoir,
euh pour calculer la dérivée de x->exp(x).sin(x) moi j'utilise juste (fg)'=fg'+f'g ...
-
Hmida
- Messages: 5
- Enregistré le: 14 Nov 2007, 14:29
-
 par Hmida » 04 Fév 2008, 20:37
par Hmida » 04 Fév 2008, 20:37
Nightmare a écrit:Bonsoir,
euh pour calculer la dérivée de x->exp(x).sin(x) moi j'utilise juste (fg)'=fg'+f'g ...
Il s'agit de la dérivée n-ème :happy2: je ne sais pas comment m'y prendre... :hum:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Fév 2008, 20:41
par Nightmare » 04 Fév 2008, 20:41
Dinstingue les cas n congru à 0, 1, 2 ou 3 modulo 4.
:happy3:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Fév 2008, 20:50
par ThSQ » 04 Fév 2008, 20:50
Nightmare a écrit:(fg)'=fg'+f'g ...
Exo : Mq qu'il existe une famille libre
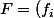_{i \in I})
de dimension infinie telle que (fg)' = f'g' pour tout f,g dans F !
:mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
