Salut à tous,
Voilà, j'ai un petit problème. On me demande de démontrer que si une suite numérique (Un) converge alors elle admet une limite unique.
Alors, mon problème se pose au niveau de la démarche à suivre!
Et je sais vraiment pas comment faire!!
En passant, svp pouvez vous m'expliquer comment on raisonne par l'absurde
Je vous remercie de votre aide.
Suites convergentes
7 messages
- Page 1 sur 1
Une suite n'admet pas forcément une seule limite, mais j'imagine que tu es dans R, auquel cas tu possède une distance qui est la valeur absolue.
Imagine que tu aies 2 limites distinctes l1 et l2.
d(l1,l2)=d>0
Pour tout e>0 il existe bla bla bla tel que
d(Un,l1)idem pour
d(Un,l2)
Puisque d=d(l1,l2)<=d(Un,l1)+d(Un,l2)
on a que d=d(l1,l2)<=e+e' c'est à dire que d(l1,l2) est aussi petit que l'on veut.
On peut trouver une contradiction dans le fait que e=e'=d/3 donne d<2d/3
Imagine que tu aies 2 limites distinctes l1 et l2.
d(l1,l2)=d>0
Pour tout e>0 il existe bla bla bla tel que
d(Un,l1)
d(Un,l2)
Puisque d=d(l1,l2)<=d(Un,l1)+d(Un,l2)
on a que d=d(l1,l2)<=e+e' c'est à dire que d(l1,l2) est aussi petit que l'on veut.
On peut trouver une contradiction dans le fait que e=e'=d/3 donne d<2d/3
nadoushka a écrit:Salut à tous,
Voilà, j'ai un petit problème. On me demande de démontrer que si une suite numérique (Un) converge alors elle admet une limite unique.
Alors, mon problème se pose au niveau de la démarche à suivre!
Et je sais vraiment pas comment faire!!
En passant, svp pouvez vous m'expliquer comment on raisonne par l'absurde
Je vous remercie de votre aide.
Une suite
et cela est impossible !
Donc l'hypothèse selon laquelle la suite a deux limites est absurde.
Un raisonnement par l'absurde consiste lorsque l'on veut démontrer une affirmation A, à supposer qu'elle est fausse et à faire des déductions successives jusqu'à aboutir à une impossibilité, ce qui montre finalement que l'hypothèse de départ selon laquelle "A est fausse", est fausse ! Et donc que A est vraie !
C'est exactement ce que j'ai fait ci-dessus. Je cherche à montrer qu'il n'y a qu'une limite. Je suppose alors qu'il y en a au moins deux distinctes a et b. Et en faisant des déductions successives, j'arrive à une impossibilité. J'ai donc montré que l'assertion "La limite n'est pas unique" est fausse (on dit souvent "absurde", mais cela n'est qu'une question de vocable). Il en résulte que j'ai montré que "la limite si elle existe est nécessairement unique"
salut nadoushka,
J'apporte ma contribution:
d'abord il faut rappeller ce que signifie qu'une suite numérique converge
On dit qu'une suite notée) converge si il existe un réél
converge si il existe un réél  tel que
tel que
 tel que
tel que <br /><br />On "applique" la définition de la convergence de la suite avec [TEX]\epsilon=\frac{d}{2}) qui est bien strictement positif.
qui est bien strictement positif.
) converge vers
converge vers  donc
donc  tel que
tel que 
Or
On arrive donc à
 , ce qui est absurde !
, ce qui est absurde !
Donc et
et 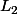 ne sont pas distinctes. Elles sont donc égales.
ne sont pas distinctes. Elles sont donc égales.
Ainsi, une suite numérique convergente admet une limite unique.
@+
:we:
J'apporte ma contribution:
d'abord il faut rappeller ce que signifie qu'une suite numérique converge
On dit qu'une suite notée
Or
On arrive donc à
Donc
Ainsi, une suite numérique convergente admet une limite unique.
@+
:we:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
