Système d'équation

[hayasdane]

bonjours, d'après cette énoncé j'ai trouvée ce système. Mais j'ai chercher et je n'y arrive pas à le résoudre. D'après les cours que j'ai fait, il faut normalement trouver un polynome du 2nd degrès, le calculer et ensuite résoudre le système. Je sais fair tout cela mais je blog au système et je n'y arrive pas a trouver le polynome du 2nd degrè qu'il faut normalement trouver.
Pouver vous m'aider silvouplais ?

[Monsieur23]

Bonjour ;

Tu peux par exemple remplacer y par 30000/x dans la deuxième équation.

Tu n'auras plus qu'une inconnue. :we:

[hayasdane]

je l'ai déja fait mais je n'y arrive pas. Je bloc quand il faut divisé par x.

[Monsieur23]

Ca te fait donc :



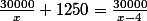
Donc

Maintenant, il faut tout mettre au même dénominateur.

[hayasdane]

mais on peut pas mètre au même dénominateur puisque à 1250 il n'y a pas de x. nan ????
Et si on peut sa n'est pas une forme d'une équation de polynome de 2nd degrès.
Enfin bon.... je ne sais pas.

...J'ai éssayé de mètre au même dénominateur mais j'y arrive pas.

[Narhm]

Bonsoir,
Déjà, il ne peux pas y avoir un nombre nul de personne sinon ca n'a pas de sens, pour ton équation où x est au dénominateur.
Bref pour reprendre ce qu'à bien commencer Monsieur23:


On prend (2) :
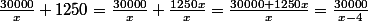
Essaie de faire le produit en croix de tout ça, tu vas tomber sur un polynôme dont tu sais trouver les racines...qui sont ?

[hayasdane]

après je trouve
(x-4)(30000+1250x)=30000x
30000x+1250x²-120000-5000x=30000x
1250x²-5000x-120000=0

délta=b²-4ac= -(5000)²-4 * 1250 * -120000 = 3100000000

après je trouve x1=-31673527.27 et x2=37923527.27

et normalement c'est x2 la bonne réponse. Mais je pense que je me suis trompé car c'est plus tot un grand nombre non ???

[Monsieur23]

En divisant tout par 1250, tu peux te ramener à l'équation x²-4-96=0

Recalcules les solutions maintenant.

Ce qui est génant dans ta réponse, c'est pas le fait que le nombre soit grand, c'est qu'il représente un nombre de personne, donc c'est un entier !

[hayasdane]

je trouve x1=-8 et x2=12
c'est donc 12 la bonne réponse. J'ai vérifier et sa marche. Merci beaucoup pour ton aide.

Juste une dérnière question... Comment est-ce-que je peut justifier le fait que je divie tout par 1250 ???

[Huppasacee]

1250x²-5000x-120000=0
Mettons 1250 en facteur , cela donne
1250 (x²-4-96)=0
Comme 1250 différent de 0, nous devons résoudre ......