Lors d'un tournoi de tennis, auquel n joueurs participent, deux joueurs jouent toujours une et une seule fois ensemble. A la fin du tournoi, chaque joueur fait une liste:il écrit le nom de chaque joueur qu'il a battu et les noms de tous ceux qui ont été battus par quelqu'un qu'il a battu.
Montrer qu'au moins un joueur a inscrit les noms de tous les autres joueurs dans sa liste.
Bon courage!
Zeb. :++:
Tournoi de tennis
32 messages
- Page 1 sur 2 - 1, 2
par Zebulon » 14 Oct 2005, 21:24
Bonsoir,
oui, évidemment! Mais ce n'est qu'une condition suffisante, on ne dit pas qu'un joueur a battu tout le monde. Le but du problème est de montrer que dans tous les cas, quelqu'un a écrit tous les autres noms sur sa liste!
oui, évidemment! Mais ce n'est qu'une condition suffisante, on ne dit pas qu'un joueur a battu tout le monde. Le but du problème est de montrer que dans tous les cas, quelqu'un a écrit tous les autres noms sur sa liste!
par Chimerade » 14 Oct 2005, 23:44
Salut !
Petite précision :
La règle du jeu est-elle récursive ? En d'autre termes, chaque joueur écrit-il seulement les joueurs qu'il a battus et ceux qui ont été battus par ceux qu'il a battu, ou doit-il également ajouter les joueurs battus par ceux que les joueurs qu'il a battu ont battu et ainsi de suite ?
Petite précision :
La règle du jeu est-elle récursive ? En d'autre termes, chaque joueur écrit-il seulement les joueurs qu'il a battus et ceux qui ont été battus par ceux qu'il a battu, ou doit-il également ajouter les joueurs battus par ceux que les joueurs qu'il a battu ont battu et ainsi de suite ?
par Zebulon » 15 Oct 2005, 06:59
Bonjour,
non, une seule fois seulement:figurent sur la liste d'un joueur les noms de ceux qu'il a battus et ceux qui ont été battus par ceux qu'il a battus.
Zeb.
non, une seule fois seulement:figurent sur la liste d'un joueur les noms de ceux qu'il a battus et ceux qui ont été battus par ceux qu'il a battus.
Zeb.
par Anonyme » 15 Oct 2005, 07:17
Prpoposition : figurent sur la liste d'un joueur les noms de ceux qu'il a battus et ceux qui ont été battus par ceux qu'il a battus.
Si G ensemble des joueurs battus par le joueur, et P ensemble des joueurs contre qui il a perdu, tel que G+P = n-1 (il ne joue pas contre lui-même),
il inscrit bien les G joueurs sur sa liste;
Je reviens à mon post précédent et une condition particulière.
Il me semble que la proposition n'est pas vraie dans tous les cas.
En effet, il y bien une condition : pour inscrire les P joueurs sur sa liste, ceux ci-doivent perdre au moins un match contre les G joueurs.
Autant les G joueurs se rencontrant entre eux, des battus battront d'autres battus (pas de match nul) mais ils sont déjà inscrits, autant rien de prédictif ne permet d'affirmer que les G joueurs battront les P joueurs.
Quelque chose m'échappe.
Si G ensemble des joueurs battus par le joueur, et P ensemble des joueurs contre qui il a perdu, tel que G+P = n-1 (il ne joue pas contre lui-même),
il inscrit bien les G joueurs sur sa liste;
Je reviens à mon post précédent et une condition particulière.
Il me semble que la proposition n'est pas vraie dans tous les cas.
En effet, il y bien une condition : pour inscrire les P joueurs sur sa liste, ceux ci-doivent perdre au moins un match contre les G joueurs.
Autant les G joueurs se rencontrant entre eux, des battus battront d'autres battus (pas de match nul) mais ils sont déjà inscrits, autant rien de prédictif ne permet d'affirmer que les G joueurs battront les P joueurs.
Quelque chose m'échappe.
par Anonyme » 15 Oct 2005, 09:45
Illumination, mais pas de démo ....
Supposons 3 joueurs A, B, C
A bat B, A bat C : A inscrit B C
A bat B, C bat A, B bat C : A inscrit B C
A bat B, C bat A, C bat B : C inscrit A B
A battu par B, A bat C, C bat B : A inscrit B C
A battu par B, A bat C, B bat C : B inscrit A C
A battu par B, A battu par C, C bat B : C inscrit A B
A battu par B, A battu par C, B bat C : B inscrit A C
CQFD sur un exemple .....
Cas particulier : cas 1 un joueur gagne tout
Autres cas : dans l'arbre, un joueur d'un match "inscrit" son adversaire et les battus de son adversaire
A chaque noeud de l'arbre, il y a héritage soit d'une branche soit de l'autre et donc de proche en proche, un joueur inscrit son adversaire et les inscrits de son adversaire.
Donc par rapport à mes ensembles G et P, G "grossit" par transfert des éléments du G du perdant présents dans le P du gagnant vers le G du gagnant (c'est pas très matheux tout ça mais je me comprends ...)
je laisse à qui veut (peut) finir.
Supposons 3 joueurs A, B, C
A bat B, A bat C : A inscrit B C
A bat B, C bat A, B bat C : A inscrit B C
A bat B, C bat A, C bat B : C inscrit A B
A battu par B, A bat C, C bat B : A inscrit B C
A battu par B, A bat C, B bat C : B inscrit A C
A battu par B, A battu par C, C bat B : C inscrit A B
A battu par B, A battu par C, B bat C : B inscrit A C
CQFD sur un exemple .....
Cas particulier : cas 1 un joueur gagne tout
Autres cas : dans l'arbre, un joueur d'un match "inscrit" son adversaire et les battus de son adversaire
A chaque noeud de l'arbre, il y a héritage soit d'une branche soit de l'autre et donc de proche en proche, un joueur inscrit son adversaire et les inscrits de son adversaire.
Donc par rapport à mes ensembles G et P, G "grossit" par transfert des éléments du G du perdant présents dans le P du gagnant vers le G du gagnant (c'est pas très matheux tout ça mais je me comprends ...)
je laisse à qui veut (peut) finir.
par Zebulon » 15 Oct 2005, 10:09
Je ne comprends pas très bien ce que vous dites. Pourriez-vous l'expliquer plus clairement s'il vous plait? J'ai l'impression que quand vous dites "de proche en proche", vous considérez que la règle du jeu est récursive comme le demandait Chimerade. Si c'est ce que vous avez cru, alors je vous arrête:ce n'est pas le cas. Mais pourquoi pas continuer de chercher sur un exemple à 4 joueurs si ça vous illumine?! :lol3:
par Patastronch » 15 Oct 2005, 22:31
Procedons par l absurde.
Supposons que le joueur J qui a ecrit le plus de nom sur sa feuille n' apas ecris tous les noms.
Soit K l'ensemble de joueurs non inscrit sur la feuille de J. Donc K est l'ensemble des joueurs qui ont battu J. Donc tous les joueurs de l'ensemble K ecrivent J plus les noms que J a ecrit sur sa feuille.
Contradiction puisque les joueurs de la liste K ecrivent plus de noms que J. Celui qui a ecrit le plus de nom sur sa feuille a donc ecrit le nom de tous les joueurs. (on déduit egalement qu'il n a ete battu par personne et qu'un tel joueur est unique).
Ca me parait trop simple j 'ai du faire une erreur quelque part mais je vois pas ou.
Supposons que le joueur J qui a ecrit le plus de nom sur sa feuille n' apas ecris tous les noms.
Soit K l'ensemble de joueurs non inscrit sur la feuille de J. Donc K est l'ensemble des joueurs qui ont battu J. Donc tous les joueurs de l'ensemble K ecrivent J plus les noms que J a ecrit sur sa feuille.
Contradiction puisque les joueurs de la liste K ecrivent plus de noms que J. Celui qui a ecrit le plus de nom sur sa feuille a donc ecrit le nom de tous les joueurs. (on déduit egalement qu'il n a ete battu par personne et qu'un tel joueur est unique).
Ca me parait trop simple j 'ai du faire une erreur quelque part mais je vois pas ou.
par Zebulon » 16 Oct 2005, 07:21
Patastronch a écrit:Procedons par l absurde.
Supposons que le joueur J qui a ecrit le plus de nom sur sa feuille n' apas ecris tous les noms.
Soit K l'ensemble de joueurs non inscrit sur la feuille de J. Donc K est l'ensemble des joueurs qui ont battu J. Donc tous les joueurs de l'ensemble K ecrivent J plus les noms que J a ecrit sur sa feuille.
Contradiction puisque les joueurs de la liste K ecrivent plus de noms que J. Celui qui a ecrit le plus de nom sur sa feuille a donc ecrit le nom de tous les joueurs. (on déduit egalement qu'il n a ete battu par personne et qu'un tel joueur est unique).
Ca me parait trop simple j 'ai du faire une erreur quelque part mais je vois pas ou.
Bonjour,
ce qui est en gras est faux! Désolée...
par becirj » 16 Oct 2005, 14:18
Le nombre maximum de noms que l'on peut inscrire est n-1.Supposons ceci non réalisé ; soit n-p (p>1) le nombre maximum de noms inscrits et A un joueur ayant inscrit ce nombre.
Soit B un joueur non inscrit par A. B a donc battu A et les n-p joueurs inscrits par A (sinon il figurerait sur la liste de A). B a donc battu n-p+1 joueurs en contadiction la supposition. Il y a au moins un joueur qui a inscrit n-1 noms.
Soit B un joueur non inscrit par A. B a donc battu A et les n-p joueurs inscrits par A (sinon il figurerait sur la liste de A). B a donc battu n-p+1 joueurs en contadiction la supposition. Il y a au moins un joueur qui a inscrit n-1 noms.
par Patastronch » 16 Oct 2005, 15:12
En effet, et la c est mieu ?
Procedons par l absurde.
Supposons que le joueur J qui a ecrit le plus de nom sur sa feuille n' apas ecris tous les noms.
Soit K l'ensemble de joueurs non inscrit sur la feuille de J. Donc K est l'ensemble des joueurs qui ont battu J. Donc tous les joueurs de l'ensemble K ecrivent J plus les noms que J a ecrit sur sa feuille.
Contradiction puisque les joueurs de la liste K ecrivent plus de noms que J. Celui qui a ecrit le plus de nom sur sa feuille a donc ecrit le nom de tous les joueurs. (on déduit egalement qu'il n a ete battu par personne et qu'un tel joueur est unique).
Explication de ce qui est en gras :
Soit L un joueur que J a ecrit sur sa feuile et que K n'a pas sur sa feuille.
Supposons que L existe :
Alors L a ete battu par un joueur battu par J (joueur M). Hors si K n a pas ecris ce nom c'est qu'il s est fait battre par L. Donc K est sur la liste de L, et donc K est sur la liste de M.
Si K a battu M alors K possede bien le nom L. Contradiction.
Si K n'a pas battu M alors M a K sur sa liste en lien direct et donc J a aussi K Impossible du a notre premiere hypothese absurde.
Procedons par l absurde.
Supposons que le joueur J qui a ecrit le plus de nom sur sa feuille n' apas ecris tous les noms.
Soit K l'ensemble de joueurs non inscrit sur la feuille de J. Donc K est l'ensemble des joueurs qui ont battu J. Donc tous les joueurs de l'ensemble K ecrivent J plus les noms que J a ecrit sur sa feuille.
Contradiction puisque les joueurs de la liste K ecrivent plus de noms que J. Celui qui a ecrit le plus de nom sur sa feuille a donc ecrit le nom de tous les joueurs. (on déduit egalement qu'il n a ete battu par personne et qu'un tel joueur est unique).
Explication de ce qui est en gras :
Soit L un joueur que J a ecrit sur sa feuile et que K n'a pas sur sa feuille.
Supposons que L existe :
Alors L a ete battu par un joueur battu par J (joueur M). Hors si K n a pas ecris ce nom c'est qu'il s est fait battre par L. Donc K est sur la liste de L, et donc K est sur la liste de M.
Si K a battu M alors K possede bien le nom L. Contradiction.
Si K n'a pas battu M alors M a K sur sa liste en lien direct et donc J a aussi K Impossible du a notre premiere hypothese absurde.
par Zebulon » 16 Oct 2005, 20:48
Bonsoir,
cette fois c'est mieux!!! D'ailleurs, ça me semble juste. On m'a posé ce problème sans que j'aie la solution, mais c'est aussi ce que j'ai trouvé. Voici la solution que je propose : soit J le joueur ayant le plus de victoires "directes", soit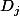
la liste des joueurs battus par J, soit 
la liste des joueurs battus indirectement par J, ie battus par des joueurs de 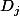. Les ont donc tous battus J.
Supposons maintenant K un joueur qui n'est pas sur la liste de J. Alors
donc K a battu J
donc K a battu chacun des joueurs de la liste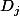
Enfin, K récupère dans sa liste, par victoires indirectes, les victoires directes des joueurs de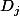, à savoir les .
Donc
car J va dans les victoires directes de K,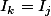 
donc liste de 
donc K a un joueur de plus sur sa liste que J, et même, plus précisément, un joueur de plus dans sa liste des joueurs battus directement, ce qui est contradictoire avec l'hypothèse.
Bravo à Chimerade qui avait trouvé la réponse en premier mais me l'a envoyée en message privé. Chimerade me pose la question suivante:à quelle condition tous les joueurs ont inscrit les noms de tous les autres joueurs sur sa liste? Je laisse le débat se poursuivre!
Merci à tous ceux qui ont cherché; c'est bien les maths! :we:
A bientôt,
Zeb. :langue2:
cette fois c'est mieux!!! D'ailleurs, ça me semble juste. On m'a posé ce problème sans que j'aie la solution, mais c'est aussi ce que j'ai trouvé. Voici la solution que je propose : soit J le joueur ayant le plus de victoires "directes", soit
Supposons maintenant K un joueur qui n'est pas sur la liste de J. Alors
Enfin, K récupère dans sa liste, par victoires indirectes, les victoires directes des joueurs de
Donc
Bravo à Chimerade qui avait trouvé la réponse en premier mais me l'a envoyée en message privé. Chimerade me pose la question suivante:à quelle condition tous les joueurs ont inscrit les noms de tous les autres joueurs sur sa liste? Je laisse le débat se poursuivre!
Merci à tous ceux qui ont cherché; c'est bien les maths! :we:
A bientôt,
Zeb. :langue2:
par lovedeschamps » 23 Oct 2005, 15:55
SAlut
au fait l enigme est evidente par recurrence sur le nombre de joueurs
au fait l enigme est evidente par recurrence sur le nombre de joueurs
par Zebulon » 23 Oct 2005, 18:35
Bonsoir,
pourriez-vous poster votre preuve évidente s'il vous plaît?
Merci,
Zeb.
pourriez-vous poster votre preuve évidente s'il vous plaît?
Merci,
Zeb.
par lovedeschamps » 23 Oct 2005, 18:45
montrons par recurrence sur n=nombre de joueurs l assertion An :
il existe un joeur ayant ecrit tous les joueurs sur la liste
n=2 Evident
supposons An montrons An+1
on prend n joueur au hasard par An il existe un joueur ki a ecrit tt les n joueurs
si ce joueur a aussi battu le restant il a donc ecrit tt le monde sur la liste
sinon le restant a ecrit tout les joueurs sur sa liste
Voila
pour l imaginer il suffit de penser a un tournoi de tennis
il existe un joeur ayant ecrit tous les joueurs sur la liste
n=2 Evident
supposons An montrons An+1
on prend n joueur au hasard par An il existe un joueur ki a ecrit tt les n joueurs
si ce joueur a aussi battu le restant il a donc ecrit tt le monde sur la liste
sinon le restant a ecrit tout les joueurs sur sa liste
Voila
pour l imaginer il suffit de penser a un tournoi de tennis
par Zebulon » 23 Oct 2005, 18:49
Ben non, le restant R pourrait très bien avoir battu V celui qui a battu les n joueurs pris au départ, sans les avoir tous battus! Certes R hérite des victoires de V, mais pas de sa liste entière...
par lovedeschamps » 23 Oct 2005, 19:49
donc un joueur ecrit juste la liste directe des battu
g cru ke ca se transmet
il fallait preciser au depart
g cru ke ca se transmet
il fallait preciser au depart
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :