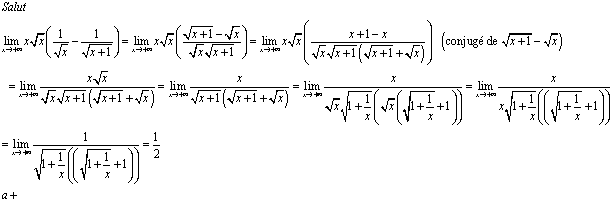Limites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 31 Jan 2008, 00:35
par juju78 » 31 Jan 2008, 00:35
(re)Bonjour, on me demande la limite en +oo de
)
Je ne vois pas comment faire pouvez vous m'aider
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 31 Jan 2008, 00:50
par Huppasacee » 31 Jan 2008, 00:50
Multiplie par la quantité conjuguée de la parenthèse ( pour avoir a² - b² )
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 31 Jan 2008, 01:00
par juju78 » 31 Jan 2008, 01:00
on obtient alors:

?
Mais apres que faire ?
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 31 Jan 2008, 01:09
par Huppasacee » 31 Jan 2008, 01:09
Après , il y a des mises sous mêmes dénominateurs qui peuvent se faire
-
smp
- Membre Relatif
- Messages: 156
- Enregistré le: 07 Mai 2007, 19:35
-
 par smp » 31 Jan 2008, 01:11
par smp » 31 Jan 2008, 01:11
c'est pas evident
toujours forme indeterminé
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 31 Jan 2008, 01:13
par juju78 » 31 Jan 2008, 01:13
ben je met au meme denominateur le denominateur de la parenthese et j'obtients:
})
mais apres je vois pas comment faire
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 31 Jan 2008, 01:19
par Huppasacee » 31 Jan 2008, 01:19
je ne sais pas comment l'écrire avec des formules maths, mais en gros j'obtiens :
x rac x / x(x+1) * racx * rac (x+1) /( racx + rac (x + 1)
pas toi ?
-
~oa~
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juil 2007, 18:38
-
 par ~oa~ » 31 Jan 2008, 01:26
par ~oa~ » 31 Jan 2008, 01:26
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 31 Jan 2008, 09:33
par juju78 » 31 Jan 2008, 09:33
mici bcp =]
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2008, 19:07
par Nightmare » 31 Jan 2008, 19:07
Bonsoir :happy3:
Ou sinon on développe :
\sqrt{x}}{\sqrt{x+1}}-\frac{\sqrt{x}}{\sqrt{x+1}}=x-\sqrt{x}\sqrt{x+1}+\sqrt{\frac{x}{x+1}})
Or :

Et si on a suivit ses cours de premières, on sait qu'il existe une fonction e qui tend vers 0 en 0 telle que :
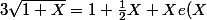)
D'où :
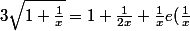)
On a alors :
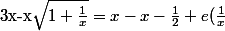=-\frac{1}{2}+e(\frac{1}{x}))
Au final :
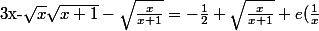 \longrightarrow_{x\to +\infty} \frac{1}{2})
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
)