Algèbre pour les bébés

[Babe]

Bonsoir

j'ai un petit souci avec cet exercice, enfin le souci c'est que je ne comprends pas la question

"Soit n réels distincts. Montrer que les fonctions
avec i=1,..,n sont linéairements indépendantes dans l'espace vectoriel "

merci d'avance

[Babe]

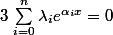
dois je montrer que avec ?

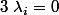
[Nightmare]

Salut :happy3:

On revient à la définition >

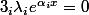
Supposons qu'il existe tels que pour tout x.

Que dire des ?

:happy3:

[Nightmare]

Non au contraire il faut montrer que si la somme est nulle, les lambda i le sont tous.

[Babe]

Non au contraire il faut montrer que si la somme est nulle, les lambda i le sont tous.

oui bien sur
me suis enflammer sur le latex :zen:

[bruce.ml]

Salut,

indépendants ça veut dire ce qu'on pense que ça veut dire : il n'existe pas de combinaison linéaire nulle de tes éléments. A une petite chose près, c'est que dans un espace vectoriel, zéro est TOUJOURS là pour nous embêter : une combinaion linéaire avec que des zéros ne pourra faire que zéro. Alors c'est pour ça qu'on prend comme définition de linéairement indépendants : si jamais on arrive à faire une combinaison linéaire nulle, et bien c'est qu'en fait on a utilisé que des zéros.

[Babe]

exp est toujours positive donc pour que la somme soit nulle les sont necessairement nul
oui ?

[Nightmare]

Lol, ça arrive.

L'idée est d'ordonner les alpha i. Quitte à permuter, on peut supposer que l'ordre est le suivant :

On écrit alors que
et en faisant tendre x vers l'infini, on a clairement que lambda n est nul. On réitère pour lambda n-1 etc...

:happy3:

[Nightmare]

Babe > Les lambda peuvent être négatifs.

[Babe]

Babe > Les lambda peuvent être négatifs.

oui....:marteau:

[Babe]

L'idée est d'ordonner les alpha i. Quitte à permuter, on peut supposer que l'ordre est le suivant :

oui je suis d'accord

On écrit alors que

par contre la je comprends pas la 1er somme (pk le x=n) et le lien avec la 2e somme

et en faisant tendre x vers l'infini, on a clairement que lambda n est nul. On réitère pour lambda n-1 etc...

oui compris


merci

[Nightmare]

Euh oui, c'est un x et non un n dans ma première somme.

bref :


:happy3:

[Babe]

Euh oui, c'est un x et non un n dans ma première somme.

bref :

super merci :++: