Somme de série

[nolucky]

Bonjour,
J'aimerai savoir comment on calcul une somme de séries et comment sait on si elle est convergente ou divergente

Voici une liste de somme de séries, pourriez vous m'expliquer par rapport à ces differentes séries :

SOMME ( de k=0 à linfini) de 1/2K
k=2007 " " " ""

somme de exp k

somme de 1
somme de k

somme de 2k

somme de ( ln(k+1)-ln(k))

[Antho07]

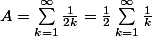
et comme la série des 1/k diverge (riemann) , A diverge.


B=somme des exp(k)
ben donc la serie diverge grossierement.

Les suivantes sont des sommes de suite arithmetique....


La derniere:

Ln(k+1)-Ln(k)=Ln ( (k+1)/k) = ln (1 +1/k).

je pense que la regle de d alembert peut s'appliquer moyennant un Dl

[bitonio]

( ln(k+1)-ln(k)) donne une série téléscopique (tous les termes s'annulent deux à deux, sauf le premier et le dernier.) La série diverge donc car ln diverge en +oo. De plus, ~ donc elle diverge aussi d'après Riemann

[bruce.ml]

La dernière est une somme téléscopique ... rien de plus simple

edit : méchant Bitonio

[Joker62]

Justement, si la série diverge, on a pas le droit de regrouper, de bouger les termes non ?