Encadrement et equivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 27 Jan 2008, 21:33
par zelda007 » 27 Jan 2008, 21:33
Salut à tous,
Soit la suite Hn = Somme(k variant de 1 à n) des 1/k
A partir de cette expression,

On me demande d'en déduire que pour tout n non nul : ln(n+1) <= Hn <= ln(n) + 1
Mais je ne vois pas du tout comment faire ca !
Merci à tous

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 27 Jan 2008, 21:57
par Nightmare » 27 Jan 2008, 21:57
Salut :happy3:
En sommant sur [1,n] non?
-
Memento
- Membre Naturel
- Messages: 71
- Enregistré le: 13 Jan 2008, 18:17
-
 par Memento » 27 Jan 2008, 22:58
par Memento » 27 Jan 2008, 22:58
ReSalut,
Tu pars d'abord de :
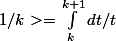
en applicant la somme de 1 a n à gauche et a droite du signe, on a
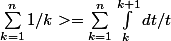
et avec :
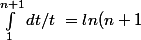)
tu devrais obtenir:
 >= ln(n+1))
-------------------------------
Après, en partant de:
 <= \int_k^{k+1} dt/t\)
et en appliquant la somme de 1 à n-1 à gauche et a droite du signe, on a:
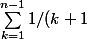 <= \sum_{k=1}^{n-1} \int_k^{k+1} dt/t\)
et avec :
)
tu devrais obtenir
 <= 1 + ln(n))
@+
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 27 Jan 2008, 23:07
par zelda007 » 27 Jan 2008, 23:07
Effectivement c'est bien vu :)
Enfin pour finir, on me demande un equivalent simple de Hn en plus l'infini. D'après le theorème des gendarmes on a deja Hn qui tends vers + l'infini mais je ne vois pas comment trouver un équivalent :hein:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 27 Jan 2008, 23:18
par fatal_error » 27 Jan 2008, 23:18
Hello,
ln(n+1)~ln(n) en linfini et ln(n)+1~ln(n)
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités

