Bonjour, je n'arrive pas à déterminer
}{\sqrt{1-t^2}}dt)
où
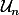
désigne l'ensemble des polynômes réels unitaires de degré
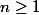
, sachant qu'il y avait une question préliminaire sur les polynômes de Tchebychev (montrer qu'il existe un unique polynôme

tel que
=T_n(\cos x))
, et qu'alors

est de degré n et son coefficient dominant est
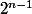
).
Sachant aussi que c'est un exo du cours sur les espaces préhilbertiens, j'ai considéré le produit scalaire sur
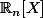
défini par
Q(t)}{\sqrt{1-t^2}}dt=\int_0^{\pi}P(\cos t)Q(\cos t)dt)
.
On a alors
}{\sqrt{1-t^2}}dt=d^2(0,\mathcal{U}_n))
Mais à partir de là, je commence à sécher, je pense que ça peut s'avérer intéressant d'écrire
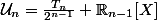
, et qu'alors on aurait :
}{\sqrt{1-t^2}}dt= \begin{Vmatrix}\frac{T_n}{2^{n-1}}\end{Vmatrix} ^2-\begin{Vmatrix}p\(\frac{T_n}{2^{n-1}}\)\end{Vmatrix}^2)
avec le p le projecteur orthogonal sur
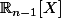
(je suis pas tout à fait sûr de cette égalité...).
J'arrive à calculer
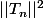
mais je ne trouve pas son projeté orthogonal sur
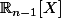
...
Merci d'avance à ceux qui pourront m'aider.
