Tribu produit

par **CC_** » 26 Jan 2008, 15:30

Hello,

Je viens juste de découvrir la notion de tribu et tout cela est encore un peu frais. J'ai une petite question à vous poser par rapport à un passage de mon cours. On nous dit :

Soient

n ensembles. On pose

.
Soit

une tribu sur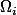

. De manière générale,

n'est pas une tribu.

J'avoue ne pas voir exactement pourquoi, puisque je ne vois pas laquelle des trois propriétés d'une tribu est mise en défaut...
Can you help me please ? :marteau:

Merci !

par **ThSQ** » 26 Jan 2008, 16:53

Il y a des cas où c'est vrai (exemple idiot :

).

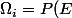Plus généralement ça peut être faux. Par analogies les ouverts de R² sont bien plus compliqués/riches que les ouverts obtenus en faisant O1 x O2

par **tize** » 27 Jan 2008, 11:04

Bonjour,
en complément de ce que ThSQ t'a déjà dit tu peux essayer de voir ce qu'il se passe dans

en faisant un dessin...
Si

et

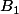
sont des segments disjoints ainsi que

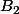
et

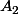
alors

dans le premier cas on a l'union de deux rectangles disjoints et dans le second on a l'union de quatre rectangles ! et il est imopssible d'écrire

comme étant égal à

par **Lierre Aeripz** » 27 Jan 2008, 15:59

ThSQ a écrit:Il y a des cas où c'est vrai (exemple idiot : ).

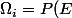Même dans ce cas là c'est faux en général

par **houda 20** » 27 Nov 2009, 18:22

c'est bizzzzzzzzzare
le matin j'ai ajouté une réponse là et je ne la retrouve pas maintenant????????????????

Tribu produit

Tribu produit

Qui est en ligne