Primitive d'un exponentiel

[bronzes]

bonsoir,
savez-vous
quelle est la primitive de exp(-x^3), j'en ai besoin pour une intégrale double.

merci d'avance
:hum:

[raito123]

C'est tout de même facile non ?

c'est

[MathMoiCa]

C'est tout de même facile non ?

c'est

Hello,

Euh...je veux bien que tu redérives ce machin pour voir si ça redonne l'expression de départ :--:



M.

[Antho07]

je ne crois pas que cela soit une fonction usuelle. On a le meme probleme que pour e^(-t²)(l integrale de gauss)

on s'en sortait avec les integrales double en passant en polaire. on en déduisait que

[bronzes]

je suis d'accord avec la premier reponse mais ce qui me genait c le X^3 ds l'exponentiel lui ne "bouge" pas, il ne change pas sa puissance?


merci ds tous les cas

[Joker62]

Non la première est fausse naturellement.
J'imagine également que c'est de la même forme que l'intégrale de Gauss.
Donc je dirais, donne ton intégrale double pour voir...

[Antho07]

C'est tout de même facile non ?

c'est

c'est pas facil du tout.

aucune fonction usuelle ne fonctionne. Celle que tu propose ne donne pas du tout e^(-t^3)

[bronzes]

int(int(exp(-x^3)dx dy et D = x compris entre 0 et 1 et y compris entre sqrt(y) et 1

[busard_des_roseaux]

Tu peux tenter les coordonnées polaires:

[Pythales]

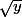
Que veut dire compris entre et ?