Bloque sur une implication
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 21 Jan 2008, 17:28
par pouik » 21 Jan 2008, 17:28
Bonsoir,
Je cherche depuis quelques heures maintenant à montrer l'implication suivante, mais sans réussite !!!!
Soient

et

deux espaces vectoriels normés. Soit

une application linéaire de

vers

. Montrer l'implication :
(1) :

est continue au point
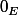
(2) : il existe un réel positif

tel que
||_F \le k ||x||_E)
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 21 Jan 2008, 18:09
par klevia » 21 Jan 2008, 18:09
Salut, est-on en dimension fini ?
-
SimonB
 par SimonB » 21 Jan 2008, 18:15
par SimonB » 21 Jan 2008, 18:15
Montre d'abord que, en supposant (1), u est alors bornée sur la boule unité (en écrivant la définition de la continuité en 0 et en fixant

. Déduis-en le résultat (indice : écrit
)
si x est un élément quelconque de E non nul...).
(pour klevia : non, en dimension finie, toute application linéaire est continue...)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Jan 2008, 18:19
par tize » 21 Jan 2008, 18:19
Bonjour, très simple :
* u continue en 0 => il existe d>0 tq ||x||<=d => ||u(x)||<1
* u(x/||x||)=1/d.u(d.x/||x||) donc pour tout x : ||u(x)||<=......
[edit] : grillé par tout le monde (ou presque) désolé... : :we:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 21 Jan 2008, 18:25
par pouik » 21 Jan 2008, 18:25
[quote="tize"]
* u(x/||x||)=1/d.u(d.x/||x||) donc pour tout x : ||u(x)||= 1 donc d.x/||x|| >= x, mais c'est tout je ne vois rein d'autre...


-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Jan 2008, 18:36
par tize » 21 Jan 2008, 18:36
Bon, je te le refais en plus clair :

continue en

donc il existe
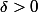
tel que
||<1)
=\frac{1}{\delta}.u\( \delta. \frac{x}{||x||} \))
et tu remarqueras que
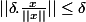
donc
||\leq 1)
donc
||\leq\frac{1}{\delta})
donc
||\leq...)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 21 Jan 2008, 19:06
par pouik » 21 Jan 2008, 19:06
donc par linéarité de la norme (non ??) :
||\leq \frac{1}{\delta} ||x||)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Jan 2008, 19:59
par tize » 21 Jan 2008, 19:59
Oui...enfin la norme n'est pas linéaire mais il est vrai que l'on a
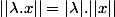
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités