Qui peut m'aider svp
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par atomic_boy_algeria » 15 Jan 2008, 22:38
par atomic_boy_algeria » 15 Jan 2008, 22:38
voila l'enoncé d'un exo que j'ai pas pu résoudre , c bét je c , mais les suites recurrentes c pas mon truc lol
soit (Un)n une suite numérique ,définie par sont par:
U0=0
et Un+1= (1-Un)²
1ere qst (facile) : montrer que 02eme qst: etudier la monotonie de (U2n) et (U2n+1), et donner leur limites si elles existent ?
3eme qstn: que peut on conclure ?
ca parré tres facile , ce qui est le cas , mais je me suis bloquer dans l'etudes de la monotonie , les suite récurrente , je me suis pas vraiment exercer dessus , j'ai tjr travailler sur les suites de fonctions,c dans l'études de la monotonie des deux sous suite que je me suis bloquer, j'ai pas trouvé l'astuce . merci d'avance
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2008, 22:40
par Nightmare » 15 Jan 2008, 22:40
Bonsoir,
peux-tu éviter le langage sms?
Merci.
 par atomic_boy_algeria » 15 Jan 2008, 22:46
par atomic_boy_algeria » 15 Jan 2008, 22:46
le langage sms , oui c'est sans blem euh non pardon sans probleme, c'est juste pour ecrire rapidement et aussi pour camoufler les fautes d'orthographe que je fais :we:
 par atomic_boy_algeria » 15 Jan 2008, 22:52
par atomic_boy_algeria » 15 Jan 2008, 22:52
je dirais que c'est standart comme exercice , mais il y a toujours une petite faille dans nos pensées , une astuce qui nous échape, j'ai bloquer a l'études de la monotonie des deux sous suite , j'ai essayé de claculer U2n+1 - U2n , j'ai essayer aussi avec U2n+1 / U2n , U2n / U2n-1 .... j'ai pas aboutie à un résulat, voila sinon pour quoi je poserai cette question la ? :ptdr:
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 15 Jan 2008, 23:07
par seriousme » 15 Jan 2008, 23:07
N'y a t'il pas une erreur dans l'énoncé car sinon :
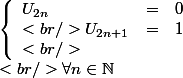
Preuve par récurrence pour U_{2n}:
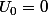
;
Soit
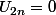
alors :
} = U_{2n + 2} = (1 - U_{2n + 1})^2 = (1 - (1 - U_{2n})^2)^2 = (1 - 1)^2 = 0)
.
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 15 Jan 2008, 23:10
par seriousme » 15 Jan 2008, 23:10
N'y a t'il pas une erreur dans l'énoncé car sinon :
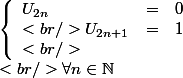
Preuve par récurrence pour
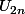
:
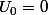
;
Soit
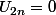
alors :
} = U_{2n + 2} = (1 - U_{2n + 1})^2 = (1 - (1 - U_{2n})^2)^2 = (1 - 1)^2 = 0)
.
 par atomic_boy_algeria » 15 Jan 2008, 23:14
par atomic_boy_algeria » 15 Jan 2008, 23:14
oui je rectefie U0 = 1/2 et non pas zéro , désolé pour ca :mur:
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 16 Jan 2008, 00:02
par seriousme » 16 Jan 2008, 00:02
A priori
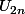
est croissante .
Preuve :
-
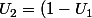^2 = (1 - \frac{1}{4})^2 = \frac{9}{16} \geq U_0)
.
-
} = U_{2n + 2} = (1 - U_{2n + 1})^2 = (1 - (1 - U_{2n})^2)^2 = (2U_{2n} - U_{2n}^2)^2 = U_{2n}(U_{2n}(2 - U_{2n})^2))
Soit
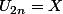
.
Or la fonction
 = X(2 - X)^2)
vaut
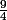
en

et 1 en 1 .
Donc
 \geq 1)
.
Or
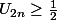
par hypothèse de récurrence .
Donc
} = aU_{2n})
avec
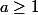
donc
} \geq U_{2n})
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
