Forme exp d'un complexe

[Aria]

Voilà, j'ai un exercice à rendre comportant des questions de a) à f) et j'ai déjà fait jusqu'à d) inclus mais e) et f) restent infaisables pour moi, j'ai tatonné au brouillon sans rien trouver alors je vous demande un peu d'aide, si vous pouvez me donner au moins des pistes, ce serait super !
Merci d'avance ^^~

Consigne: Ecrivez z sous forme exponentielle et déduisez-en la forme algébrique de z barre et 1/z .

[Skullkid]

Bonjour, les termes en exponentielle sont déjà sous forme voulue, donc ce qui pose problème ce sont les nombres complexes mis sous forme algébriques et élevées à des puissances diverses.

D'abord, sans t'occuper de la puissance à laquelle ils sont élevés, essaye d'écrire ces nombres sous forme exponentielle.

Par exemple, , est-ce que tu ne verrais pas comment l'écrire sous forme exponentielle simplement ? (Rappel : ).

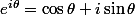
[Aria]

J'ai réussi le e) grace à ta méthode, merci beaucoup !
J'ai aussi réussi à la réappliquer pour le f) seulement après multiplication par les puissances, cela me donne un truc bizarre:



Je pense que j'ai du faire une erreur qq part mais je n'arrive pas à trouver où... :hein:

[Skullkid]

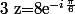
Sûrement une erreur de calcul, pour le f j'obtiens (mais je suis pas à l'abri d'erreurs non plus !)

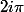
Autre chose : quand tu as des arguments moches genre , essaye de les mettre sous une forme plus simple (en ajoutant ou retranchant des multiples de ). Par exemple

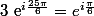
[Aria]

Bon ça fait 4 fois que je refais le calcul... et je trouve à chaque fois une réponse différente, et maintenant j'ai plus qu'à tirer à la courte paille ? ^^"

Plus sérieusement, quel theta tu trouves pour la partie (1-i)^4 ?
Parce que je crois que c'est ça qui me pose problème... >,<

[Skullkid]

J'avais d'ailleurs fait une erreur dans mon calcul, on doit tomber sur

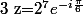
[Aria]

Je trouve comme toi sauf tout à la fin, je trouve:



Chez moi le - s'annule par un autre - quand je divise les exponentielles.

[Skullkid]

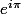
Il y a bien un -, quand tu divises par c'est comme si tu multipliais par , donc tu ajoutes à l'argument.

[Aria]

J'ai à peu près compris pour f) ^^"
Il me reste une dernière question à propos d'un autre exo, le voici:



C'est la question 3 qui me reste, j'ai calculé l'équation de la tangente en A et je sais que pour que celle ci soit parallèle à (BC), il faut le même coefficient directeur, mais après ça, je ne vois pas quel calcul effectuer... :triste:

Merci d'avance.

[Memento]

Salut,

1.a.

f(x)=Ln(exp(-x)*(exp(x) + 1))
= -x + Ln(1+exp(x))


1.b

f(x)/x = -1 + Ln(1+exp(x))/x

Lim (-inf) f(x)/x = -1

asymptote y=-x en (-inf)

2.

Derivé(f(x))= -1/(1+ exp(x)) < 0 ; Vx élément de R

f décroissante sur R

3.

A(0,ln(2)) ; B(1, Ln(1+1/e)) ; C(-1, Ln(1+e))

pente tangente en A = Derive(f)(0)=-1/2

Vect(tangente) = Vect (U) = (-2,1)

calcul du déterminant (devant être nul)

Det(Vect(u), Vect(BC))= (-2, 1) . (-2, ln(1+e)-ln(1+1/e))
= 0


@+