Arithmétique pgcd

[raptor77]

Bonjour les ami(e)s j'ai un petit problème avec un bout de mon exercice
Il faut que je retrouve le pgcd de 2n+1 et n-5 mais je n'y arrive pas.
Je serais reconnaissant de votre aide
merci d'avance
Cordialement
Raptor

[J-R]

bonsoir,



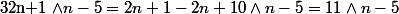
donc 2 possibilitées possibles à déterminer suivant n ...

[raptor77]

bonsoir,



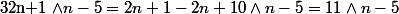
donc 2 possibilitées possibles à déterminer suivant n ...

d'où vient le -2n+10?on a le droit d'enlever comme ca? et comment je fais pour trouver pgcd(11;n-5) en fonction de n?

[raptor77]

:hum: personne?

[J-R]

on utilise la propriété suivante:

( et a et b non simultanément nul)
et pour tout entier k, on a:



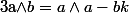
(c'est sur cette propriété qu'est basé l'algo d'euclide )


pour ton exemple:

{}

donc



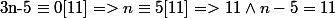
et si n-5 n'est pas un multiple de 11 alors le pgcd est 1.

[raptor77]

merci beaucoup

Une dernière question coment tu fais pour prouver que si n-5 n'est pas un multiple de 11 le pgcd c'est 1?

[J-R]

c'est trivial on va dire.

s'il n'est pas un multiple de 11 alors comme 11 est premier ils n'admettent aucun diviseur commun autre que 1.