Problème de compréhension sur les limites
23 messages
- Page 1 sur 2 - 1, 2
Problème de compréhension sur les limites
Bonjour,
ayant quitté le lycée il y a déjà un certain moment et n'ayant pas réutilisé depuis tout le savoir que j'y avais accumulé, je me retrouve aujourd'hui confronté à un problème de compréhension vis-à-vis de l'expression suivante. Excusez moi par avance du manque de lisibilité de la formule. J'ai bien essayé de la copier/coller à partir de Word, mais cela n'a pas fonctionné.
Somme (t=1 à infini) (Z / ((1+i)^t)) = lim (T tend vers infini) Somme (t=1 à T) (Z / ((1+i)^t) = Z / i
Je n'arrive pas à voir le cheminement qui mène à lim = Z / i. Mais très faibles souvenirs dans ce domaine m'auraient plutôt fait pencher pour lim = 0. Si quelqu'un pouvait m'éclairer...
Merci d'avance
Aurel
ayant quitté le lycée il y a déjà un certain moment et n'ayant pas réutilisé depuis tout le savoir que j'y avais accumulé, je me retrouve aujourd'hui confronté à un problème de compréhension vis-à-vis de l'expression suivante. Excusez moi par avance du manque de lisibilité de la formule. J'ai bien essayé de la copier/coller à partir de Word, mais cela n'a pas fonctionné.
Somme (t=1 à infini) (Z / ((1+i)^t)) = lim (T tend vers infini) Somme (t=1 à T) (Z / ((1+i)^t) = Z / i
Je n'arrive pas à voir le cheminement qui mène à lim = Z / i. Mais très faibles souvenirs dans ce domaine m'auraient plutôt fait pencher pour lim = 0. Si quelqu'un pouvait m'éclairer...
Merci d'avance
Aurel
C'est vrai qu'on me dit de ne pas parler de suite géométrique parce qu'elle n'est pas au programme mais mtn je dois le faire mdr ben voilà:
au passage de premier terme est evident pour ne pas mettre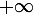 en haut en pose limte de T en + infini et on remplace le plus infinie en haut par le T.
en haut en pose limte de T en + infini et on remplace le plus infinie en haut par le T.
Pour le passage du 2éme terme au 3éme voilà :
considérant la suite^n})
si on calcul Un+1 on ca se rencontrer que c'est une suite géométrique de raison et mtn c'est facile je suppose???
et mtn c'est facile je suppose???
au passage de premier terme est evident pour ne pas mettre
Pour le passage du 2éme terme au 3éme voilà :
considérant la suite
si on calcul Un+1 on ca se rencontrer que c'est une suite géométrique de raison
Les multiples ne doivent pas être utilisés sans nécessité
Aureletudiant a écrit:Pour le passage du premier au second terme, ok, je vois. Pour le passage du second au troisième, je rejette un coup d'oeil sur les suites géométriques et je reviens.
Oui c'est mieux essaie de revoir comment faire la somme des termes d'une suite géometrique
Les multiples ne doivent pas être utilisés sans nécessité
Bon, c'est bien laborieux tout ça. Après moulte calcul: je bloque à ce niveau là:
Sn = Somme des n premiers termes
Sn = (z / i ) * (((1+i)^(n+1)) - 1) / ((1+i)^n)
j'ai bien le z / i mais je commence à tourner en rond pour faire disparaître la seconde partie de formule.
Je mettrais bien les calculs qui m'ont menés jusqu'à ce résultat, mais je crains que ce ne soit trop indigeste à lire...
Sn = Somme des n premiers termes
Sn = (z / i ) * (((1+i)^(n+1)) - 1) / ((1+i)^n)
j'ai bien le z / i mais je commence à tourner en rond pour faire disparaître la seconde partie de formule.
Je mettrais bien les calculs qui m'ont menés jusqu'à ce résultat, mais je crains que ce ne soit trop indigeste à lire...
Bon ok, mais j'aurai prévenu:
Pour une suite géométrique, on a:
Un = U0 * q^n
Appliqué à notre formule => Un = z * (1/(1+i)^n)
U0 = z
Sn = z + (z/(1+i))+...+ (z/(1+i)^n)
qSn= (z/(1+i))+...+(z/(1+i)^(n+1))
Sn-qSn= (1-q)Sn
(1-q)Sn = z - (z/(1+i)^(n+1))
(1-q)Sn = z * (1- (1/(1+i)^(n+1))
Sn = z * (1- (1/(1+i)^(n+1)) / (1-q)
Sn = z * (1- (1/(1+i)^(n+1)) / (1- (1/(1+i))
Sn = z * (1- (1/(1+i)^(n+1)) / (i/(1+i))
Sn = (z/i) * (1/(1+i)^(n+1)) * (1+i)
Sn = (z/i) * ((((1+i)^(n+1))-1)/ ((1+i)^(n+1))) * (1+i)
Sn = (z/i) * (((1+i)^(n+1))-1)/ ((1+i)^n)
Et voilà ! ...mais maintenant, je sèche....
Pour une suite géométrique, on a:
Un = U0 * q^n
Appliqué à notre formule => Un = z * (1/(1+i)^n)
U0 = z
Sn = z + (z/(1+i))+...+ (z/(1+i)^n)
qSn= (z/(1+i))+...+(z/(1+i)^(n+1))
Sn-qSn= (1-q)Sn
(1-q)Sn = z - (z/(1+i)^(n+1))
(1-q)Sn = z * (1- (1/(1+i)^(n+1))
Sn = z * (1- (1/(1+i)^(n+1)) / (1-q)
Sn = z * (1- (1/(1+i)^(n+1)) / (1- (1/(1+i))
Sn = z * (1- (1/(1+i)^(n+1)) / (i/(1+i))
Sn = (z/i) * (1/(1+i)^(n+1)) * (1+i)
Sn = (z/i) * ((((1+i)^(n+1))-1)/ ((1+i)^(n+1))) * (1+i)
Sn = (z/i) * (((1+i)^(n+1))-1)/ ((1+i)^n)
Et voilà ! ...mais maintenant, je sèche....
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
