DM sur dérivation 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 04 Jan 2008, 14:49
par ALFRED78 » 04 Jan 2008, 14:49
Bonjour ayant commencé la dérivation en cours je ne connait pas beaucoup de technique. Quelqu'un pourrait-il m'aidait?
Merci d'avance, voici l'exercice.

-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 04 Jan 2008, 15:58
par ALFRED78 » 04 Jan 2008, 15:58
personne pour de l'aide? S'il vous plait.
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 04 Jan 2008, 16:36
par andros06 » 04 Jan 2008, 16:36
Bonjour,
pour cet exo il n' y a pas besoin de connaître de techniques specifiques à la dérivation. Il s'agit uniquement de calculs bêtes et méchants.
Qu'as-tu fait ?
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 04 Jan 2008, 16:47
par ALFRED78 » 04 Jan 2008, 16:47
J'ai developpé mais je ne tombe pas sur les bonnes formules,
je tombe sur (1-V(1+h))²/(-2h) pour la première question
V= racine carrée
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 05 Jan 2008, 13:41
par ALFRED78 » 05 Jan 2008, 13:41
Malgré une seule réponse m'indiquant que l'exercice est simple sans me donner plus d'information, je suis toujours englué dans mon exercice de dérivation. Il ya t'il une bonne ame pour au moins me dire comment débuter dans l'exercice.
L'exercice est donné ci-dessous dans mon message d'hier.
Merci d'avance à tous.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 05 Jan 2008, 14:10
par fonfon » 05 Jan 2008, 14:10
suite à ton MP
=\sqrt{1+h})
et est-ce que c'est
=\frac{f(h)-f(0)}{h}-\frac{1}{2})
? je vois mal sur la l'ecran
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 05 Jan 2008, 14:16
par ALFRED78 » 05 Jan 2008, 14:16
oui c'est bien ça
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 05 Jan 2008, 14:34
par fonfon » 05 Jan 2008, 14:34
donc
je calcule deja
-f(0)}{h})
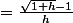
(\sqrt{1+h}+1)}{h(\sqrt{1+h}+1)})
^2-1}{h(\sqrt{1+h}+1)})
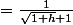
apres simplification
donc maintenant
-f(0)}{h}-\frac{1}{2})
(on va reduir au même denominateur)
=
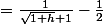
=
})
=
})
et là tu refait encore l'expression conjuguée
=
(1+\sqrt{1+h})}{2(\sqrt{1+h}+1)(\sqrt{1+h}+1)})
=
^2}{2(\sqrt{1+h}+1)(\sqrt{1+h}+1)})
=
^2})
je te laisse poursuivre les autres questions
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 05 Jan 2008, 15:52
par ALFRED78 » 05 Jan 2008, 15:52
Merci beaucoup, je vais poursuivre.
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 05 Jan 2008, 21:18
par ALFRED78 » 05 Jan 2008, 21:18
Je suis arrivée a la question 3 mais je me retrouve bloqué en cherchant comment faire.
J'ai chercher si la fonction était dérivable et j'ai trouvé qu'elle l'était en 0.
Je suis alors parti de la formule:
f(a+h)= f(a)+ hf'(a)+hE(h)
( avec E= epsilon et V= racine carrée)
et je tombe sur:
f(h)=1+ V(1+h) -1 +hE(h)
Mais je ne sais pas comment arriver sur le 1/2h de l'énoncer,le V(1+h) -1 me bloque.Est-ce quelqu'un pourait me donner une indication.
Merci d'avance.
-
ALFRED78
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Jan 2008, 15:57
-
 par ALFRED78 » 06 Jan 2008, 11:42
par ALFRED78 » 06 Jan 2008, 11:42
bonjour, ce matin j'ai fini le DM excepté cette question, ca serait simpa si quelqu'un pouvait me donner une indication.
Merci d'avance
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités

